
 二次函數y=$\frac{2}{3}$x2的函數圖象如圖,點A0位于坐標原點,點A1,A2,A3…A10 在y軸的正半軸上,點B1,B2,B3…B10在二次函數y=$\frac{2}{3}$x2位于第一象限的圖象上,△A0B1A1,△A1B2A2,△A2B3A3…△A9B10A10都為等邊三角形,則△A9B10A10的邊長為10.
二次函數y=$\frac{2}{3}$x2的函數圖象如圖,點A0位于坐標原點,點A1,A2,A3…A10 在y軸的正半軸上,點B1,B2,B3…B10在二次函數y=$\frac{2}{3}$x2位于第一象限的圖象上,△A0B1A1,△A1B2A2,△A2B3A3…△A9B10A10都為等邊三角形,則△A9B10A10的邊長為10. 分析 根據等邊三角形的性質可得∠A1A0B1=60°,然后表示出A0B1的解析式,與二次函數解析式聯立求出點B1的坐標,再根據等邊三角形的性質求出A0A1,同理表示出A1B2的解析式,與二次函數解析式聯立求出點B2的坐標,再根據等邊三角形的性質求出A1A2,同理求出B3的坐標,然后求出A2A3,從而得到等邊三角形的邊長為從1開始的連續自然數,與三角形所在的序數相等.
解答 解:∵△A0B1A1是等邊三角形,
∴∠A1A0B1=60°,
∴A0B1的解析式為y=$\frac{\sqrt{3}}{3}$x,
聯立$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x}\\{y=\frac{2}{3}{x}^{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=\frac{\sqrt{3}}{2}}\\{{y}_{1}=\frac{1}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=0}\\{{y}_{2}=0}\end{array}\right.$(為原點,舍去),
∴點B1($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),
∴等邊△A0B1A1的邊長為$\frac{1}{2}$×2=1,
同理,A1B2的解析式為y=$\frac{\sqrt{3}}{3}$x+1,
聯立$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x+1}\\{y=\frac{2}{3}{x}^{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=\sqrt{3}}\\{{y}_{1}=2}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-\frac{\sqrt{3}}{2}}\\{{y}_{2}=\frac{1}{2}}\end{array}\right.$(在第二象限,舍去),
∴B2($\sqrt{3}$,2),
∴等邊△A1B2A2的邊長A1A2=2×(2-1)=2,
同理可求出B3($\frac{3\sqrt{3}}{2}$,$\frac{9}{2}$),
所以,等邊△A2B3A3的邊長A2A3=2×($\frac{9}{2}$-1-2)=3,
…,
以此類推,系列等邊三角形的邊長為從1開始的連續自然數,
△A9B10A10的邊長A9A10=10.
故答案為:10.
點評 本題考查了二次函數圖象上點的坐標特征,等邊三角形的性質,主要利用了聯立兩函數解析式求交點坐標,根據點B系列的坐標求出等邊三角形的邊長并且發現系列等邊三角形的邊長為從1開始的連續自然數是解題的關鍵.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案 全優沖刺100分系列答案
全優沖刺100分系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
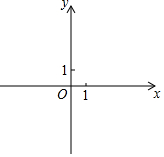 設點Q到圖形W上每一個點的距離的最小值稱為點Q到圖形W的距離.例如正方形ABCD滿足A(1,0),B(2,0),C(2,1),D(1,1),那么點O(0,0)到正方形ABCD的距離為1.
設點Q到圖形W上每一個點的距離的最小值稱為點Q到圖形W的距離.例如正方形ABCD滿足A(1,0),B(2,0),C(2,1),D(1,1),那么點O(0,0)到正方形ABCD的距離為1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
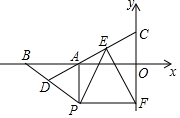 已知:如圖,平面直角坐標系中,點B坐標為(-4,0),點A為線段OB中點,點P在第三象限,且AP⊥y軸,PF⊥y軸,D為BP中點,連接DA并延長交y軸于點C,FE⊥DC.
已知:如圖,平面直角坐標系中,點B坐標為(-4,0),點A為線段OB中點,點P在第三象限,且AP⊥y軸,PF⊥y軸,D為BP中點,連接DA并延長交y軸于點C,FE⊥DC.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
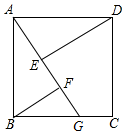 在邊長為4cm的正方形ABCD中,點G是射線CB上的一點,E、F為直線AG上兩個動點,連接DE、BF.
在邊長為4cm的正方形ABCD中,點G是射線CB上的一點,E、F為直線AG上兩個動點,連接DE、BF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
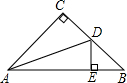 如圖,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于點D,DE⊥AB交AB于點E,AB=4$\sqrt{2}$cm,求△BDE的周長.
如圖,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于點D,DE⊥AB交AB于點E,AB=4$\sqrt{2}$cm,求△BDE的周長.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com