
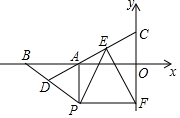
 已知:如圖,平面直角坐標系中,點B坐標為(-4,0),點A為線段OB中點,點P在第三象限,且AP⊥y軸,PF⊥y軸,D為BP中點,連接DA并延長交y軸于點C,FE⊥DC.
已知:如圖,平面直角坐標系中,點B坐標為(-4,0),點A為線段OB中點,點P在第三象限,且AP⊥y軸,PF⊥y軸,D為BP中點,連接DA并延長交y軸于點C,FE⊥DC.分析 (1)根據點B的坐標以及中點的定義即可解決問題.
(2)只要證明△PBA≌△CAO即可.
(3)如圖延長PE交y軸于M.由△PAE≌△MCE,推出EP=EM,由∠PFM=90°,推出EF=PE(直角三角形的斜邊上的中線等于斜邊的一半).
解答 (1)解:∵B(-4,0),AB=OA,
∴點A坐標為(-2,0).
故答案為(-2,0)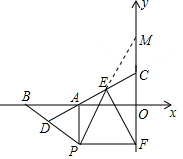
(2)證明:∵PA⊥AB,
∴∠BAP=∠AOC=90°,
∵BD=DP,
∴AD=DB=PD,
∴∠ABP=∠BDA=∠CAO,
在△PBA和△CAO中,
$\left\{\begin{array}{l}{∠PAB=∠AOC}\\{AB=AO}\\{∠ABP=∠CAO}\end{array}\right.$,
∴△PBA≌△CAO,
∴PB=CA.
(3)解:結論:△PEF是等腰三角形.
理由:如圖延長PE交y軸于M.
∵PA∥CM,
∴∠PAE=∠MCE,
在△PAE和△MCE中,
$\left\{\begin{array}{l}{∠PAE=∠MCE}\\{AE=EC}\\{∠AEP=∠CEM}\end{array}\right.$,
∴△PAE≌△MCE,
∴EP=EM,
∵∠PFM=90°,
∴EF=PE(直角三角形的斜邊上的中線等于斜邊的一半).
∴△PEF是等腰三角形.
點評 本題考查三角形綜合題、全等三角形的判定和性質、直角三角形斜邊中線的性質等知識,解題的關鍵是學會添加常用輔助線,構造全等三角形解決問題,屬于中考常考題型.


 手拉手全優練考卷系列答案
手拉手全優練考卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
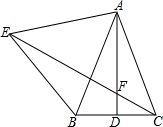 如圖,△ABC中,AB=AC,AD是BC邊上的中線,以AB為邊向外作等邊△ABE,與直線AD交于點F.
如圖,△ABC中,AB=AC,AD是BC邊上的中線,以AB為邊向外作等邊△ABE,與直線AD交于點F.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 二次函數y=$\frac{2}{3}$x2的函數圖象如圖,點A0位于坐標原點,點A1,A2,A3…A10 在y軸的正半軸上,點B1,B2,B3…B10在二次函數y=$\frac{2}{3}$x2位于第一象限的圖象上,△A0B1A1,△A1B2A2,△A2B3A3…△A9B10A10都為等邊三角形,則△A9B10A10的邊長為10.
二次函數y=$\frac{2}{3}$x2的函數圖象如圖,點A0位于坐標原點,點A1,A2,A3…A10 在y軸的正半軸上,點B1,B2,B3…B10在二次函數y=$\frac{2}{3}$x2位于第一象限的圖象上,△A0B1A1,△A1B2A2,△A2B3A3…△A9B10A10都為等邊三角形,則△A9B10A10的邊長為10.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
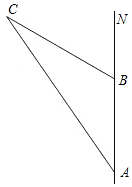 某輪船上午8時從A島出發,以20海里/小時的速度向正北方向航行,如圖,上午10時到達B島,此時得到消息,在C島周圍15海里內有暗礁,經測量得∠NAC=15°,∠NBC=30°,問該輪船繼續向北航行有無觸礁危險?
某輪船上午8時從A島出發,以20海里/小時的速度向正北方向航行,如圖,上午10時到達B島,此時得到消息,在C島周圍15海里內有暗礁,經測量得∠NAC=15°,∠NBC=30°,問該輪船繼續向北航行有無觸礁危險?查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com