
 如圖,大正方形的邊長為a,小正方形的邊長為b.
如圖,大正方形的邊長為a,小正方形的邊長為b.分析 (1)根據題意和圖形可知陰影部分的面積是大正方形的面積加上小正方形的面積再減去△AGF和△ACD的面積,然后用相應的代數式表示出來即可解答本題;
(2)將(1)中S的代數式變形,然后將a+b=4,ab=2,代入即可解答本題.
解答 解:(1)由圖可得,
陰影部分的面積S是:${a}^{2}+{b}^{2}-\frac{{a}^{2}}{2}-\frac{(a+b)b}{2}$=$\frac{{a}^{2}}{2}+\frac{{b}^{2}}{2}-\frac{ab}{2}$,
即陰影部分的面積S是$\frac{{a}^{2}}{2}+\frac{{b}^{2}}{2}-\frac{ab}{2}$;
(2)∵a+b=4,ab=2,
∴S=$\frac{{a}^{2}}{2}+\frac{{b}^{2}}{2}-\frac{ab}{2}$=$\frac{{a}^{2}+{b}^{2}}{2}-\frac{ab}{2}$=$\frac{(a+b)^{2}-2ab}{2}-\frac{ab}{2}$=$\frac{{4}^{2}-2×2}{2}-\frac{2}{2}$=5,
即如果a+b=4,ab=2,S的值是5.
點評 本題考查整式的混合運算、代數式求值,解題的關鍵是明確題意,用相應的代數式表示出陰影部分的面積,會求代數式的值.


科目:初中數學 來源: 題型:解答題
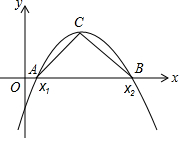 如圖,拋物線y=(1-m)x2+4x-3的開口向下,與x軸交于A(x1,0),B(x2,0)兩點,其中x1≤x2
如圖,拋物線y=(1-m)x2+4x-3的開口向下,與x軸交于A(x1,0),B(x2,0)兩點,其中x1≤x2查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 4 | B. | $2\sqrt{5}$ | C. | $\frac{{18\sqrt{3}}}{13}$ | D. | $\frac{{12\sqrt{3}}}{13}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
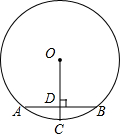 如圖,AB為⊙O的弦,AB=6cm,OC⊥AB于D,交⊙O于點C,且CD=1cm,則⊙O的半徑為( )
如圖,AB為⊙O的弦,AB=6cm,OC⊥AB于D,交⊙O于點C,且CD=1cm,則⊙O的半徑為( )| A. | 5cm | B. | 6cm | C. | 8cm | D. | 10cm |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,C為射線AB上一點,AB=30,AC比BC的$\frac{1}{4}$多5,P,Q兩點分別從A,B兩點同時出發.分別以2單位/秒和1單位/秒的速度在射線AB上沿AB方向運動,運動時間為t秒,M為BP的中點,N為QM的中點,以下結論:
如圖,C為射線AB上一點,AB=30,AC比BC的$\frac{1}{4}$多5,P,Q兩點分別從A,B兩點同時出發.分別以2單位/秒和1單位/秒的速度在射線AB上沿AB方向運動,運動時間為t秒,M為BP的中點,N為QM的中點,以下結論:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com