
分析 理解min{a,b}的含義就是取二者中的較小值,畫出函數圖象草圖,利用函數圖象的性質可得結論.
解答 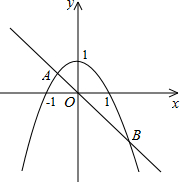 解:在同一坐標系xOy中,畫出函數二次函數y=-x2+1與正比例函數y=-x的圖象,如圖所示.設它們交于點A、B.
解:在同一坐標系xOy中,畫出函數二次函數y=-x2+1與正比例函數y=-x的圖象,如圖所示.設它們交于點A、B.
令-x2+1=-x,即x2-x-1=0,解得:x=$\frac{1+\sqrt{5}}{2}$或$\frac{1-\sqrt{5}}{2}$,
∴A($\frac{1-\sqrt{5}}{2}$,$\frac{\sqrt{5}-1}{2}$),B($\frac{1+\sqrt{5}}{2}$,$\frac{-1-\sqrt{5}}{2}$).
觀察圖象可知:
①當x≤$\frac{1-\sqrt{5}}{2}$時,min{-x2+1,-x}=-x2+1,函數值隨x的增大而增大,其最大值為$\frac{\sqrt{5}-1}{2}$;
②當$\frac{1-\sqrt{5}}{2}$<x<$\frac{1+\sqrt{5}}{2}$時,min{-x2+1,-x}=-x,函數值隨x的增大而減小,其最大值為$\frac{\sqrt{5}-1}{2}$;
③當x≥$\frac{1+\sqrt{5}}{2}$時,min{-x2+1,-x}=-x2+1,函數值隨x的增大而減小,最大值為$\frac{-1-\sqrt{5}}{2}$.
綜上所示,min{-x2+1,-x}的最大值是$\frac{\sqrt{5}-1}{2}$.
故答案:$\frac{\sqrt{5}-1}{2}$.
點評 本題考查了二次函數與正比例函數的圖象與性質,充分理解定義min{a,b}和掌握函數的性質是解題的關鍵.


 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:初中數學 來源: 題型:選擇題
| A. | a3-b | B. | $\frac{{a}^{3}}{b}$ | C. | 3a-b | D. | $\frac{3a}{b}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
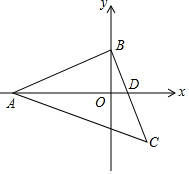 如圖,在等腰Rt△ABC中,∠ABC=90°,A(p,0),B(0,r),點C在第四象限,BC與x軸交于點D(q,0),x軸恰好平分∠BAC,則點C的坐標為( )
如圖,在等腰Rt△ABC中,∠ABC=90°,A(p,0),B(0,r),點C在第四象限,BC與x軸交于點D(q,0),x軸恰好平分∠BAC,則點C的坐標為( )| A. | (r,$\frac{p-q}{2}$) | B. | (-$\frac{p}{2}$,$\frac{p-q}{2}$) | C. | (r,p+q) | D. | (2q,$\frac{p-r}{2}$) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 自來水銷售價格 | 污水處理價格 | |
| 每戶每月用水量 | 單價:元/噸 | 單價:元/噸 |
| 17噸及以下 | a | 0.80 |
| 超過17噸不超過30噸的部分 | b | 0.80 |
| 超過30噸的部分 | 6.00 | 0.80 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,半徑為5的⊙O中,弦AB,CD所對的圓心角分別是∠AOB,∠COD.已知CD=6,∠AOB+∠COD=180°,則弦AB的弦心距等于3.
如圖,半徑為5的⊙O中,弦AB,CD所對的圓心角分別是∠AOB,∠COD.已知CD=6,∠AOB+∠COD=180°,則弦AB的弦心距等于3.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com