
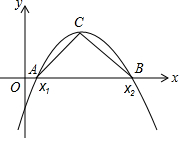
 如圖,拋物線y=(1-m)x2+4x-3的開口向下,與x軸交于A(x1,0),B(x2,0)兩點,其中x1≤x2
如圖,拋物線y=(1-m)x2+4x-3的開口向下,與x軸交于A(x1,0),B(x2,0)兩點,其中x1≤x2分析 (1)根據題意可以得到關于m的不等式組,從而可以求得m的取值范圍;
(2)根據x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=10和根與系數的關系可以得到m的值,從而可以求得此拋物線的解析式;
(3)根據等腰直角三角形的性質,可以得到m的值,從而可以求得相應的拋物線的解析式.
解答 解:(1)∵拋物線y=(1-m)x2+4x-3的開口向下,與x軸交于A(x1,0),B(x2,0)兩點,其中x1≤x2,
∴$\left\{\begin{array}{l}{1-m<0}\\{{4}^{2}-4×(1-m)×(-3)≥0}\end{array}\right.$,
解得,1<m$≤\frac{7}{3}$,
即m的取值范圍是:1<m$≤\frac{7}{3}$;
(2)∵(1-m)x2+4x-3=0時,兩根為x1,x2,
∴${x}_{1}+{x}_{2}=-\frac{4}{1-m}$,${x}_{1}{x}_{2}=\frac{-3}{1-m}$,
∵x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=10,
∴$({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}$=10,
即$(-\frac{4}{1-m})^{2}-2×\frac{-3}{1-m}$=10,
解得,${m}_{1}=-\frac{5}{3}$(舍去),m2=2,
∴拋物線的解析式為:y=-x2+4x-3;
(3)∵點C為拋物線的頂點,△ABC為等腰直角形,
∴$\frac{{x}_{2}-{x}_{1}}{2}=\frac{4(1-m)×(-3)-{4}^{2}}{4×(1-m)}$,
∵$({x}_{2}-{x}_{1})^{2}=({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}$,
即$({x}_{2}-{x}_{1})^{2}=(-\frac{4}{1-m})^{2}-4×\frac{-3}{1-m}$,
∴${x}_{2}-{x}_{1}=\frac{2\sqrt{7-3m}}{m-1}$,
∴$\frac{\sqrt{7-3m}}{m-1}=\frac{4(1-m)×(-3)-{4}^{2}}{4×(1-m)}$,
解得,${m}_{1}=\frac{7}{3}$,m2=1(舍去),
∴m=$\frac{7}{3}$,
∴拋物線的解析式為:y=$(1-\frac{7}{3}){x}^{2}+4x-3$=$-\frac{4}{3}{x}^{2}+4x-3$,
即拋物線的解析式為:y=$-\frac{4}{3}{x}^{2}+4x-3$.
點評 本題考查拋物線與x軸的交點、用待定系數法求二次函數解析式、等腰直角三角形的性質,解題的關鍵是明確題意,找出所求問題需要的條件,明確二次函數的性質.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | AC=BC | B. | AB=2AC | C. | AC+BC=AB | D. | $BC=\frac{1}{2}AB$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (a-4)(a+4)=a2-4 | B. | (4xy+1)(4xy-1)=16x2y2-1 | ||
| C. | (2x-3)(x+3)=2x2-9 | D. | (x+2)(x+2)=x2+4 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
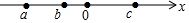 實數a,b,c在數軸上對應的點如圖,則下列式子中正確的是( )
實數a,b,c在數軸上對應的點如圖,則下列式子中正確的是( )| A. | a-c>b-c | B. | ac>bc | C. | a+c<b+c | D. | $\frac{a}{b}$<$\frac{c}{b}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | a3-b | B. | $\frac{{a}^{3}}{b}$ | C. | 3a-b | D. | $\frac{3a}{b}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | l經過定點(1,0) | B. | l經過定點(-1,0) | ||
| C. | l經過第二、三、四象限 | D. | l經過第一、二、三象限 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com