
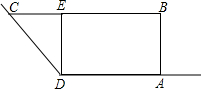
 某農場擬建一個梯形飼養場ABCD,其中AD,CD分別靠現有墻DM,DN,其余用新墻砌成,墻DM長為9米,墻DN足夠長,兩面墻形成的角度為135°,新墻DE將飼養場隔成△CDE和矩形ABED兩部分.已知新建墻體總長為30米.設AB=x米,梯形飼養場ABCD的面積為S米2.
某農場擬建一個梯形飼養場ABCD,其中AD,CD分別靠現有墻DM,DN,其余用新墻砌成,墻DM長為9米,墻DN足夠長,兩面墻形成的角度為135°,新墻DE將飼養場隔成△CDE和矩形ABED兩部分.已知新建墻體總長為30米.設AB=x米,梯形飼養場ABCD的面積為S米2.分析 (1)根據矩形和等腰直角三角形的性質得出AB=DE=CE=x米,AD=BE=30-3x米,再由矩形和三角形的面積公式可得S關于x的函數解析式;
(2)由墻DM長為9米得出x的取值范圍,再將函數解析式配方成頂點式,根據二次函數的性質可得最值情況.
解答 解:(1)∵四邊形ABED是矩形,
∴AB=CE=x米,∠ADE=∠DEC=90°,
∵∠ADC=135°,
∴∠EDC=∠DCE=45°,
∴CE=DE=x米,
∴BE=30-3x米,
∴S=x(30-3x)+$\frac{1}{2}$x2=-$\frac{5}{2}$x2+30x;
(2)∵30-3x≤9,
∴x≥7,
S=-$\frac{5}{2}$x2+30x=-$\frac{5}{2}$(x-6)2+90,
∵當x>6時,S隨x的增大而減小,
∴當x=7時,Smax=87.5,
答:當x=7時,飼料場ABCD的面積最大,最大面積為87.5平方米.
點評 本題主要考查二次函數的應用,熟練掌握矩形和等腰直角三角形的性質得出函數解析式和二次函數的性質是解題的關鍵.


科目:初中數學 來源: 題型:解答題
 點A、B在數軸上分別表示有理數a、b,A、B兩點之間的距離表示為AB,則在數軸上A、B兩點之間的距離AB=|a-b|.
點A、B在數軸上分別表示有理數a、b,A、B兩點之間的距離表示為AB,則在數軸上A、B兩點之間的距離AB=|a-b|.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
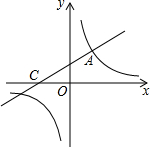 直線y=$\frac{1}{2}$x+2與雙曲線y=$\frac{k}{x}$相交于點A(2,3).
直線y=$\frac{1}{2}$x+2與雙曲線y=$\frac{k}{x}$相交于點A(2,3).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| x | … | -1 | 0 | 2 | 3 | 4 | … |
| y | … | 5 | 2 | 2 | 5 | 10 | … |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
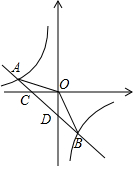 如圖,在平面直角坐標系中,一次函數y=ax-1(a≠0)的圖象與x軸交于點C,與y軸交于點D,與反比例函數y=$\frac{k}{x}$(k≠0)的圖象交于第二、四象限內的A、B兩點,點B的坐標是(3,m),連接OB,tan∠BOD=$\frac{3}{4}$.
如圖,在平面直角坐標系中,一次函數y=ax-1(a≠0)的圖象與x軸交于點C,與y軸交于點D,與反比例函數y=$\frac{k}{x}$(k≠0)的圖象交于第二、四象限內的A、B兩點,點B的坐標是(3,m),連接OB,tan∠BOD=$\frac{3}{4}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com