
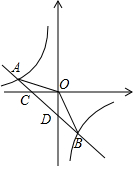
 如圖,在平面直角坐標系中,一次函數y=ax-1(a≠0)的圖象與x軸交于點C,與y軸交于點D,與反比例函數y=$\frac{k}{x}$(k≠0)的圖象交于第二、四象限內的A、B兩點,點B的坐標是(3,m),連接OB,tan∠BOD=$\frac{3}{4}$.
如圖,在平面直角坐標系中,一次函數y=ax-1(a≠0)的圖象與x軸交于點C,與y軸交于點D,與反比例函數y=$\frac{k}{x}$(k≠0)的圖象交于第二、四象限內的A、B兩點,點B的坐標是(3,m),連接OB,tan∠BOD=$\frac{3}{4}$.分析 (1)過點B作BE⊥y軸于點E,在Rt△BOE中,根據已知的三角函數值,得到點B的坐標,代入一次函數解析式中求出一次函數的解析式;
(2)把點B的坐標代入反比例函數解析式中得到反比例函數的解析式,與一次函數解析式聯立求出點A的坐標,再求出OC的長,最后利用三角形的面積公式求出△AOC與△BOC的面積,相加得到△AOB的面積,那么S△ACP=3S△AOB.然后分三種情況進行討論:①點P在x軸上方;②點P在線段OD上;③點P在點D下方.
解答 解:(1)過點B作BE⊥y軸于點E,
在Rt△BOE中,∵tan∠BOE=$\frac{BE}{OE}$=$\frac{3}{4}$,點B的坐標是(3,m),
∴B(3,-4),m=-4,
把B(3,-4)代入一次函數y=ax-1中,
得3a-1=-4,解得a=-1,
∴一次函數的解析式為y=-x-1;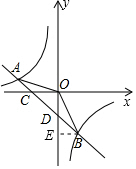 (2)把B(3,-4)代入反比例函數y=$\frac{k}{x}$中,
(2)把B(3,-4)代入反比例函數y=$\frac{k}{x}$中,
解得:k=-12,
則反比例函數的解析式為y=-$\frac{12}{x}$.
將y=-x-1代入y=-$\frac{12}{x}$,得-x-1=-$\frac{12}{x}$,
整理得,x2+x-12=0,
解得x1=3,x2=-4,
當x1=3時,y1=-4,
當x2=-4時,y2=3,
∴A(-4,3). ∵一次函數y=-x-1(a≠0)的圖象與x軸交于點C,
∵一次函數y=-x-1(a≠0)的圖象與x軸交于點C,
∴令y=0,得x=-1,∴C(-1,0),OC=1,
∴S△AOB=S△AOC+S△BOC=$\frac{1}{2}$×1×3+$\frac{1}{2}$×1×4=3.5,
∴S△ACP=3S△AOB=10.5.
設點P的坐標為(0,y).
①如果點P在x軸上方,過點A作AM⊥x軸于M,
∵S△ACP=S梯形AMOP-S△ACM-S△OCP,
∴$\frac{1}{2}$(3+y)×4-$\frac{1}{2}$×3×3-$\frac{1}{2}$×1×y=10.5,
解得y=6,
∴P(0,6);
②如果點P在線段OD上, ∵S△ACP<S△AOD=$\frac{1}{2}$×1×4=2<10.5,
∵S△ACP<S△AOD=$\frac{1}{2}$×1×4=2<10.5,
∴點P不可能在線段OD上;
③如果點P在點D下方,過點A作AN⊥y軸于N,
∵S△ACP=S△APN-S△OCP-S梯形ONAC,
∴$\frac{1}{2}$(3-y)×4-$\frac{1}{2}$×1×(-y)-$\frac{1}{2}$(1+4)×3=10.5,
解得y=-8,
∴P(0,-8).
綜上所述,所求點P的坐標為(0,6)或(0,-8).
點評 此題考查了反比例函數與一次函數的交點問題,三角形函數定義,以及三角形的面積公式的運用,用待定系數法確定函數的解析式,是常用的一種解題方法.同學們要熟練掌握這種方法.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
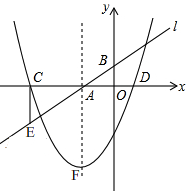 如圖1,直線l:y=mx+n交x軸,y軸于點A,B,拋物線與x軸交于點C、D,對稱軸經過點A,頂點F的縱坐標為-3.CE⊥x軸交直線l于點E(-5,-$\frac{3}{2}$),tan∠BAD=$\frac{1}{2}$.
如圖1,直線l:y=mx+n交x軸,y軸于點A,B,拋物線與x軸交于點C、D,對稱軸經過點A,頂點F的縱坐標為-3.CE⊥x軸交直線l于點E(-5,-$\frac{3}{2}$),tan∠BAD=$\frac{1}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
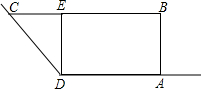 某農場擬建一個梯形飼養場ABCD,其中AD,CD分別靠現有墻DM,DN,其余用新墻砌成,墻DM長為9米,墻DN足夠長,兩面墻形成的角度為135°,新墻DE將飼養場隔成△CDE和矩形ABED兩部分.已知新建墻體總長為30米.設AB=x米,梯形飼養場ABCD的面積為S米2.
某農場擬建一個梯形飼養場ABCD,其中AD,CD分別靠現有墻DM,DN,其余用新墻砌成,墻DM長為9米,墻DN足夠長,兩面墻形成的角度為135°,新墻DE將飼養場隔成△CDE和矩形ABED兩部分.已知新建墻體總長為30米.設AB=x米,梯形飼養場ABCD的面積為S米2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
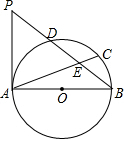 如圖所示,AB為⊙O的直徑,D為$\widehat{AC}$的中點,AC、BD交于點E,P為BD延長線上一點,且PD=DE.
如圖所示,AB為⊙O的直徑,D為$\widehat{AC}$的中點,AC、BD交于點E,P為BD延長線上一點,且PD=DE.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com