
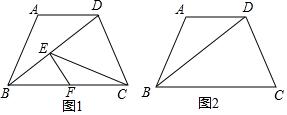
分析 (1)過A作AH⊥BD于H,再根據AD∥BC,AB=AD=5,可得∠ABD=∠ADB=∠DBC,BH=HD,再根據tan∠ABD=$\frac{3}{4}$,計算出BH=DH=4,進而得到BD=8;
(2)分兩種情況用銳角三角函數計算即可得出結論.
(3)首先利用平行線的性質得出△FEB∽△CDB,即可得出y與x的函數關系式;
解答 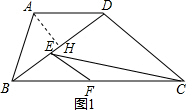 解:(1)如圖1,過A作AH⊥BD于H,
解:(1)如圖1,過A作AH⊥BD于H,
∵AD∥BC,AB=AD=5,
∴∠ABD=∠ADB=∠DBC,BH=HD,
在Rt△ABH中,
∵tan∠ABD=tan∠DBC=$\frac{3}{4}$,
∴cos∠ABD=$\frac{BH}{AB}=\frac{4}{5}$,
∴BH=DH=4,
∴BD=8;
(2)∵△DCE是等腰三角形,且BC=BD=8,
∴①如圖2,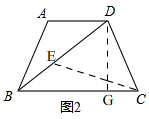 當CD=DE時,即:CD=DE=BD-BE=8-x,
當CD=DE時,即:CD=DE=BD-BE=8-x,
過點D作DG⊥BC于G,
在Rt△BDG中,tan∠DBC=$\frac{3}{4}$,BD=8,
∴DG=$\frac{3}{5}$BD=$\frac{24}{5}$,BG=$\frac{4}{5}$BD=$\frac{32}{5}$,
∴CG=8-BG=$\frac{8}{5}$,
在Rt△CDG中,根據勾股定理得,DG2+CG2=CD2,
∴($\frac{24}{5}$)2+($\frac{8}{5}$)2=(8-x)2,
∴x=8+$\frac{8\sqrt{10}}{5}$(舍)或x=8-$\frac{8\sqrt{10}}{5}$,
②如圖3, 當CE=CD時,
當CE=CD時,
過點C作CG⊥BD,
∴DG=EG=$\frac{1}{2}$DE,
在Rt△BCG中,BC=8,tan∠DBC=$\frac{3}{4}$,
∴BG=$\frac{32}{5}$,
∴DG=BD-BG=$\frac{8}{5}$,
∴x=BE=BD-DE=BD-2DG=$\frac{24}{5}$.
(3)如圖4,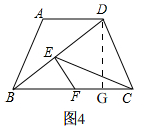 過點D作DG⊥BC于G,
過點D作DG⊥BC于G,
在Rt△BDG中,tan∠DBC=$\frac{3}{4}$,BD=8,
∴DG=$\frac{24}{5}$,BG=$\frac{32}{5}$,
∴CG=BC-BG=$\frac{18}{5}$,
在Rt△CDG中,根據勾股定理得,CD=6,
在△BCD中,BD=8,BC=10,CD=6,
∴△BCD是直角三角形,
∵EF∥CD,
∴∠BEF=∠BDC=90°,
在R△BEF中,tan∠DBC=$\frac{3}{4}$,BE=x,
∴BF=$\frac{5}{4}$x
∵BC=10,
∴FC=10-$\frac{5}{4}$x,
∴$\frac{{S}_{△FEC}}{{S}_{△EFB}}=\frac{FC}{BF}$=$\frac{10-\frac{5}{4}x}{\frac{5}{4}x}$,
∵EF∥DC,
∴△FEB∽△CDB,
∴$\frac{{S}_{△FEB}}{{S}_{△BDC}}=(\frac{BF}{BC})^{2}$=($\frac{\frac{5}{4}x}{10}$)2,
∴$\frac{{S}_{△FEC}}{{S}_{△BDC}}$=$\frac{10-\frac{5}{4}x}{\frac{5}{4}x}$•($\frac{\frac{5}{4}x}{10}$)2=-$\frac{1}{64}$x2+$\frac{1}{8}$x(0<x<8)
點評 此題是四邊形綜合題,主要考查了銳角三角函數的定義,等腰三角形的性質,勾股定理,相似三角形的性質和判定,同高的三角形的面積的比等于底的比,分類討論是解本題的關鍵,是一道比較典型的中考常考題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
 有理數a、b、c在數軸上的位置如圖所示,化簡|a-b|+|c-a|-|b-c|的結果是( )
有理數a、b、c在數軸上的位置如圖所示,化簡|a-b|+|c-a|-|b-c|的結果是( )| A. | -2a | B. | -2b | C. | -2a-2b | D. | 2a-2b |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 已知二次函數y=ax2+bx+c的圖象如圖所示,則下列結論正確的個數為( )
已知二次函數y=ax2+bx+c的圖象如圖所示,則下列結論正確的個數為( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
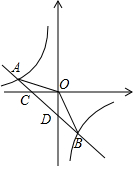 如圖,在平面直角坐標系中,一次函數y=ax-1(a≠0)的圖象與x軸交于點C,與y軸交于點D,與反比例函數y=$\frac{k}{x}$(k≠0)的圖象交于第二、四象限內的A、B兩點,點B的坐標是(3,m),連接OB,tan∠BOD=$\frac{3}{4}$.
如圖,在平面直角坐標系中,一次函數y=ax-1(a≠0)的圖象與x軸交于點C,與y軸交于點D,與反比例函數y=$\frac{k}{x}$(k≠0)的圖象交于第二、四象限內的A、B兩點,點B的坐標是(3,m),連接OB,tan∠BOD=$\frac{3}{4}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com