

分析 (1)連接BF,在FE上截取FH=BF,連接BH,易證△ABF≌△ACF,即可求得BF=CF、∠ACF=∠ABF,進而可以求證△EBH≌△ABF,即可求得EH=AF,即可求得EF的長;
(2)設∠BAD=∠CAD=α、∠ACE=∠AEC=β,得∠CAE=180°-2β、∠BAE=2α+180-2β=60°,從而知∠BAD=∠BEF,在AF上截取AG=EF,連接BG、BF,證△ABG≌△EBF得AG=EF、BG=BF,即可知△BFG為等邊三角形,可得AF=AG+GF=BF+EF=2DF+EF.
解答 解:(1)連接BF,在FE上截取FH=BF,連接BH,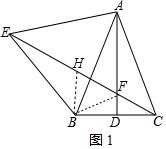
∵AB=AC,AD是BC中線,
∴∠BAD=∠CAD,
在△ABF和△ACF中,
∵$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAD}\\{AF=AF}\end{array}\right.$,
∴△ABF≌△ACF(SAS),
∴BF=CF,∠ACF=∠ABF,
∵AC=AB=AE,
∴∠ACF=∠AEF,
∴∠ABF=∠AEF,
∴∠BFH=∠EAB=60°,
∴△BFH為等邊三角形,∠BFC=120°,
∴∠FBH=∠EBA=60°,FC=$\frac{DF}{cos∠DFC}$=6,
∴∠ABF=∠EBH,
在△EBH和△ABF中,
∵$\left\{\begin{array}{l}{EB=AB}\\{∠ABF=∠EBH}\\{HB=FB}\end{array}\right.$,
∴△EBH≌△ABF(SAS),
∴EH=AF=10,
∴EF=EH+HF=AF+FC=16;
(2)AF=2DF+EF,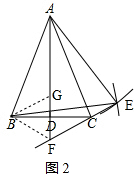
∵△ABE為等邊三角形,AB=AC,
∴AE=AB=AC,
設∠BAD=∠CAD=α,∠ACE=∠AEC=β,
∴∠CAE=180°-2β,
∴∠BAE=2α+180-2β=60°,
∴∠BAD=∠BEF,
在AF上截取AG=EF,連接BG、BF,
在△ABG和△EBF中,
∵$\left\{\begin{array}{l}{AB=EB}\\{∠BAG=∠BEF}\\{AG=EF}\end{array}\right.$,
∴△ABG≌△EBF(SAS),
∴AG=EF,BG=BF,
∴△BFG為等邊三角形,
∴AF=AG+GF=BF+EF=2DF+EF,
故答案為:AF=2DF+EF.
點評 本題考查了全等三角形的判定,考查了全等三角形對應邊、對應角相等的性質,本題中求證△ABF≌△ACF和△EBH≌△ABF是解題的關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
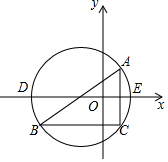 如圖,在平面直角坐標系內,已知點A(2,2),B(-6,-4),C(2,-4).
如圖,在平面直角坐標系內,已知點A(2,2),B(-6,-4),C(2,-4).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 打折前一次性購物總金額 | 優惠措施 |
| 不超過300元 | 不優惠 |
| 超過300元且不超過400元 | 售價打九折 |
| 超過400元 | 售價打八折 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
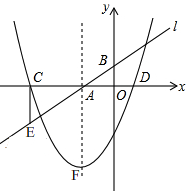 如圖1,直線l:y=mx+n交x軸,y軸于點A,B,拋物線與x軸交于點C、D,對稱軸經過點A,頂點F的縱坐標為-3.CE⊥x軸交直線l于點E(-5,-$\frac{3}{2}$),tan∠BAD=$\frac{1}{2}$.
如圖1,直線l:y=mx+n交x軸,y軸于點A,B,拋物線與x軸交于點C、D,對稱軸經過點A,頂點F的縱坐標為-3.CE⊥x軸交直線l于點E(-5,-$\frac{3}{2}$),tan∠BAD=$\frac{1}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com