
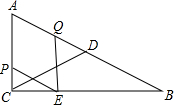
 如圖,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,CD是△ABC的中線,動點P從點C出發(fā),沿CA以每秒1個單位長度的速度向終點A運動,同時,動點Q從點A出發(fā),沿AB以每秒2個單位長度向終點B運動,過點P作PE∥AB,連結(jié)EQ,設(shè)點P運動的時間為t(s)(t>0)
如圖,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,CD是△ABC的中線,動點P從點C出發(fā),沿CA以每秒1個單位長度的速度向終點A運動,同時,動點Q從點A出發(fā),沿AB以每秒2個單位長度向終點B運動,過點P作PE∥AB,連結(jié)EQ,設(shè)點P運動的時間為t(s)(t>0)分析 (1)首先證明四邊形APEQ是平行四邊形,根據(jù)AP=AQ列出方程即可解決問題.
(2)分兩種情形討論,列出方程即可解決問題.
(3)分兩種情形①如圖3中,當0<t≤1時,重疊部分是△EMN,易知△EMN是等邊三角形.②如圖4中,當1<t≤2時,重疊部分是四邊形MNEQ.作PH⊥CD于H,延長EQ交CD的延長線于G.分別求解即可.
(4)求出圖5、圖6中兩個特殊位置的t的值,即可判斷.
解答 解:(1)在Rt△ABC中,∵∠ACB=90°,∠B=30°,AC=2,
∴AB=2AC=4,BC=2$\sqrt{3}$,
∵PE∥AB,
∴∠PEC=∠B=30°,
∴PE=2t,EC=$\sqrt{3}$t,
由題意PC=t,AQ=2t,
∴AQ=PE,∵AQ=PE,
∴四邊形APEQ是平行四邊形,
當AP=AQ時,四邊形APEQ是菱形,則2-t=2t,
∴t=$\frac{2}{3}$,
∴t=$\frac{2}{3}$時,四邊形APEQ是菱形.
(2)如圖1中,當∠QPE=90°,在Rt△APQ中,易知AP=2AQ,即2-t=4t,解得t=$\frac{2}{5}$.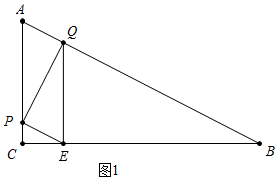
如圖2中,當∠PQE=90°,易知四邊形PQEC是矩形,可得AQ=2AP,即2t=2(2-t),解得t=1.
當∠PEQ=90°時,易知cos∠B=$\frac{\sqrt{3}}{2}$,
∴$\frac{4-2t}{2\sqrt{3}-\sqrt{3}t}=\frac{\sqrt{3}}{2}$,解得t=2,是增根,
∴此種情形不存在.
綜上所述,t=$\frac{2}{5}$s或1s時,△PQE是直角三角形.
(3)①如圖3中,當0<t≤1時,重疊部分是△EMN,易知△EMN是等邊三角形,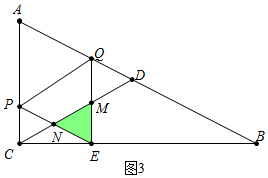
∵AD=DB,∠ACB=90°,∠B=30°,
∴CD=AD=DB,
∴∠PCN=∠CPN=60°,∠DCB=∠B=∠NEC=30°,
∴PN=EN=t,
∴S=$\frac{\sqrt{3}}{4}$t2
②如圖4中,當1<t≤2時,重疊部分是四邊形MNEQ.作PH⊥CD于H,延長EQ交CD的延長線于G.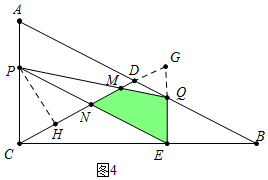
易知PC=CN=NG=EG=t,EQ=2-t,GQ=2t-2,PH=$\frac{\sqrt{3}}{2}$t,
∵GQ∥PC,
∴$\frac{GQ}{PC}$=$\frac{GM}{MC}$=$\frac{2t-2}{t}$,
∴MG=$\frac{2t-2}{3t-2}$•2t,MN=t-$\frac{2t(2t-2)}{3t-2}$,
∴S=S△PQE-S△PMN=$\frac{1}{2}$•(2-t)•$\sqrt{3}$t-$\frac{1}{2}$•[t-$\frac{2t(2t-2)}{3t-2}$]•$\frac{\sqrt{3}}{2}$t=-$\frac{\sqrt{3}}{4}$t2+$\sqrt{3}$t+$\frac{2\sqrt{3}{t}^{3}-2\sqrt{3}{t}^{2}}{6t-4}$.
(4)①如圖5中,當點A的對稱點A′在線段AB上時,易知AP=2AQ,2-t=4t,解得t=$\frac{2}{5}$.
②如圖6中,當點A的對稱點A′與點E重合時,易知AP=AQ,2-t=2t,解得t=$\frac{2}{3}$,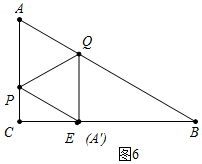
觀察圖象可知,當$\frac{2}{5}$<t<$\frac{2}{3}$時,點A′落在△ABC的外部.
點評 本題考查四邊形綜合題、菱形的判定和性質(zhì)、直角三角形的性質(zhì)、多邊形的面積問題、軸對稱等知識,解題的關(guān)鍵是靈活運用所學(xué)知識,學(xué)會用分類討論的思想思考問題,學(xué)會尋找特殊點解決問題,屬于中考壓軸題.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應(yīng)用題卡系列答案
口算與應(yīng)用題卡系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
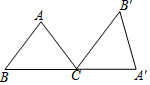 如圖,在△ABC中,AB=AC=5,BC=6,將△ABC繞點C順時針方向旋轉(zhuǎn)一定角度后得到△A′B′C.若點A′恰好落在BC的延長線上,則點B′到BA′的距離為$\frac{24}{5}$.
如圖,在△ABC中,AB=AC=5,BC=6,將△ABC繞點C順時針方向旋轉(zhuǎn)一定角度后得到△A′B′C.若點A′恰好落在BC的延長線上,則點B′到BA′的距離為$\frac{24}{5}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
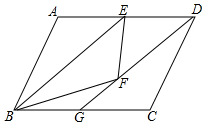 如圖,?ABCD中,E為AD邊的中點,把△ABE沿BE翻折,得到△FBE,連接DF并延長交BC于G.
如圖,?ABCD中,E為AD邊的中點,把△ABE沿BE翻折,得到△FBE,連接DF并延長交BC于G.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
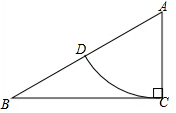 如圖,在△ABC中,∠ACB=90°,AC=1,AB=2,以A為圓心,以AC為半徑畫弧,交AB于D,則扇形CAD的周長是$\frac{π}{3}$+2(結(jié)果保留π)
如圖,在△ABC中,∠ACB=90°,AC=1,AB=2,以A為圓心,以AC為半徑畫弧,交AB于D,則扇形CAD的周長是$\frac{π}{3}$+2(結(jié)果保留π)查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com