
分析 根據題意畫出圖形,根據正六邊形的性質求出中心角,根據等邊三角形的性質、正弦的概念計算即可.
解答 解:連接正六變形的中心O和兩個頂點D、E,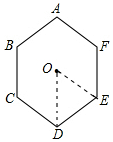 得到△ODE,
得到△ODE,
∵正六邊形的周長是12,
∴正六邊形的邊長是2,
∵∠DOE=360°×$\frac{1}{6}$=60°,OD=OE,
∴∠ODE=∠OED=(180°-60°)÷2=60°,
則三角形ODE為正三角形,
∴OD=OE=DE=2,
∴S△ODE=$\frac{1}{2}$×DE•OE•sin60°=$\frac{1}{2}$×2×2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
正六邊形的面積為6×$\sqrt{3}$=6$\sqrt{3}$.
故答案為:6$\sqrt{3}$.
點評 本題考查學生對正多邊形的概念掌握和計算的能力,不僅要熟悉正六邊形的性質,還要熟悉正三角形的面積公式.


科目:初中數學 來源: 題型:選擇題
| A. | 3.85x=67.6 | B. | 18×2.9+3.85(x-18)=67.6 | ||
| C. | 18×2.9+3.85x=67.6 | D. | 18×2.9+3.85(25-x)=67.6 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
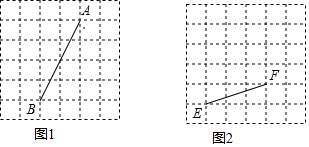
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
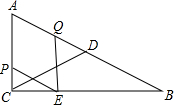 如圖,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,CD是△ABC的中線,動點P從點C出發,沿CA以每秒1個單位長度的速度向終點A運動,同時,動點Q從點A出發,沿AB以每秒2個單位長度向終點B運動,過點P作PE∥AB,連結EQ,設點P運動的時間為t(s)(t>0)
如圖,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,CD是△ABC的中線,動點P從點C出發,沿CA以每秒1個單位長度的速度向終點A運動,同時,動點Q從點A出發,沿AB以每秒2個單位長度向終點B運動,過點P作PE∥AB,連結EQ,設點P運動的時間為t(s)(t>0)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
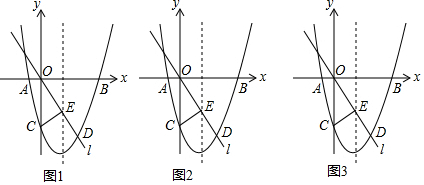
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
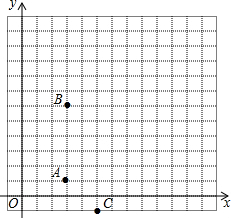 某城市的街道恰好呈東西與南北橫縱交錯格局(如圖所示),一次,警察局電子監控器屏幕上發現一輛作案后的小轎車正在點A(3,1)處以每分鐘0.5個單位長度的速度向北逃竄,根據各街道的交通狀況進行分析,逃犯很可能逃到點B(3,6)后改為向東逃竄,此時正在點C(5,-1)處巡邏的警車接到指令后立即以每分鐘0.7個單位長度的速度進行追捕,逃犯將在什么地方被追捕到?
某城市的街道恰好呈東西與南北橫縱交錯格局(如圖所示),一次,警察局電子監控器屏幕上發現一輛作案后的小轎車正在點A(3,1)處以每分鐘0.5個單位長度的速度向北逃竄,根據各街道的交通狀況進行分析,逃犯很可能逃到點B(3,6)后改為向東逃竄,此時正在點C(5,-1)處巡邏的警車接到指令后立即以每分鐘0.7個單位長度的速度進行追捕,逃犯將在什么地方被追捕到?查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com