
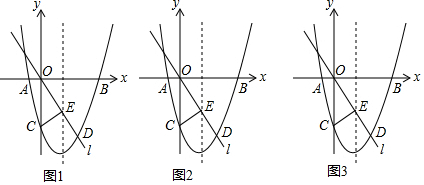
分析 (1)待定系數法求解可得;
(2)求得直線l的解析式和拋物線對稱軸即可得出交點坐標;
(3)根據△FOB和△EOB共底且面積相等可得yF=yE,即$\frac{1}{2}$x2-3x-8=-4,解之可得答案;
(4)①如圖1中,當OP=OQ時,△OPQ是等腰三角形,過點E作直線ME∥PB,交y軸于點M,交x軸于點H,求出點M、H的坐標即可解決問題.②如圖2中,當QO=QP時,△POQ是等腰三角形,先證明CE∥PQ,根據平行線的性質列出方程即可解決問題.
解答 解:(1)將點A(-2,0)、D(6,-8)代入y=ax2+bx-8,
得:$\left\{\begin{array}{l}{4a-2b-8=0}\\{36a+6b-8=-8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-3}\end{array}\right.$,
∴拋物線的函數表達式為y=$\frac{1}{2}$x2-3x-8;
(2)設直線l的解析式為y=kx,
將D(6,-8)代入,得:6k=-8,
解得:k=-$\frac{4}{3}$,
∴直線l的解析式為y=-$\frac{4}{3}$x,
又拋物線的對稱軸為x=-$\frac{-3}{2×\frac{1}{2}}$=3,
∴點E的坐標為(3,-4);
(3)存在,
設點F(x,$\frac{1}{2}$x2-3x-8),
∵S△FOB=S△EOB,即$\frac{1}{2}$OB•yF=$\frac{1}{2}$OB•yE,
∴yF=yE,即$\frac{1}{2}$x2-3x-8=-4,
解得:x=3±$\sqrt{17}$,
∴點F的坐標為(3-$\sqrt{17}$,-4)或(3+$\sqrt{17}$,-4).
(4))①如圖1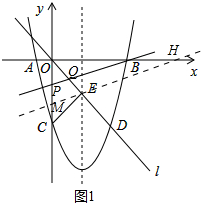
當OP=OQ時,△OPQ是等腰三角形.
∵點E坐標(3,-4),
∴OE=$\sqrt{{3}^{2}+{4}^{2}}$=5,過點E作直線ME∥PB,交y軸于點M,交x軸于點H.則$\frac{OM}{OP}$=$\frac{OE}{OQ}$,
∴OM=OE=5,
∴點M坐標(0,-5).
設直線ME的解析式為y=k1x-5,
∴3k1-5=-4,
∴k1=$\frac{1}{3}$,
∴直線ME解析式為y=$\frac{1}{3}$x-5,
令y=0,得$\frac{1}{3}$x-5=0,解得x=15,
∴點H坐標(15,0),
∵MH∥PB,
∴$\frac{OP}{OM}$=$\frac{OB}{OH}$,即$\frac{-m}{5}$=$\frac{8}{15}$,
∴m=-$\frac{8}{3}$,
②如圖2,
當QO=QP時,△POQ是等腰三角形.
∵當x=0時,y=$\frac{1}{2}$x2-3x-8=-8,
∴點C坐標(0,-8),
∴CE=$\sqrt{{3}^{2}+(8-4)^{2}}$=5,
∴OE=CE,
∴∠1=∠2,
∵QO=QP,
∴∠1=∠3,
∴∠2=∠3,
∴CE∥PB,
設直線CE交x軸于N,解析式為y=k2x-8,
∴3k2-8=-4,
∴k2=$\frac{4}{3}$,
∴直線CE解析式為y=$\frac{4}{3}$x-8,
令y=0,得$\frac{4}{3}$x-8=0,
∴x=6,
∴點N坐標(6,0),
∵CN∥PB,
∴$\frac{OP}{OC}$=$\frac{OB}{ON}$,
∴$\frac{-m}{8}$=$\frac{8}{6}$,
∴m=-$\frac{32}{3}$.
③OP=PQ時,顯然不可能,理由,
∵D(6,-8),
∴∠1<∠BOD,
∵∠OQP=∠BOQ+∠ABP,
∴∠PQO>∠1,
∴OP≠PQ,
綜上所述,當m=-$\frac{8}{3}$或-$\frac{32}{3}$時,△OPQ是等腰三角形.
點評 本題考查二次函數綜合題、一次函數的性質、待定系數法,等腰三角形的判定和性質等知識,解題的關鍵是學會分類討論,不能漏解,學會用方程的思想思考問題,屬于中考壓軸題.


 發散思維新課堂系列答案
發散思維新課堂系列答案科目:初中數學 來源: 題型:填空題
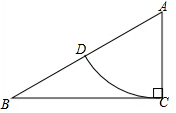 如圖,在△ABC中,∠ACB=90°,AC=1,AB=2,以A為圓心,以AC為半徑畫弧,交AB于D,則扇形CAD的周長是$\frac{π}{3}$+2(結果保留π)
如圖,在△ABC中,∠ACB=90°,AC=1,AB=2,以A為圓心,以AC為半徑畫弧,交AB于D,則扇形CAD的周長是$\frac{π}{3}$+2(結果保留π)查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在正方形ABCD中,△BPC是等邊三角形,BP、CP的延長線分別交AD于點E、F,連結BD、DP.下列結論:
如圖,在正方形ABCD中,△BPC是等邊三角形,BP、CP的延長線分別交AD于點E、F,連結BD、DP.下列結論:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
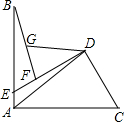 已知:AB=AC,DC=DF,∠BAC=∠CDF=90°,點G在BF上,
已知:AB=AC,DC=DF,∠BAC=∠CDF=90°,點G在BF上,查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com