
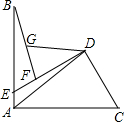
 已知:AB=AC,DC=DF,∠BAC=∠CDF=90°,點(diǎn)G在BF上,
已知:AB=AC,DC=DF,∠BAC=∠CDF=90°,點(diǎn)G在BF上,分析 (1)如圖,延長AG到M使得GM=AG,連接BM、AF、DA、DM,延長MF交AB于N.只要證明△ACD≌△MFD,即可推出DM=AD,∠ADC=∠MDF,推出∠MDA=∠FDC=90°,推出△ADM是等腰直角三角形,由AG=GM,推出AG⊥DG AG=DG.
(2)如圖2中,過點(diǎn)A作AM⊥AD交DG的延長線于M,連接MB延長MB交CD的延長線于N,連接MF、BD、AF、AD.只要證明△MAB≌△DAC,四邊形BDFM是平行四邊形,即可解決問題.
解答 證明:(1)如圖,延長AG到M使得GM=AG,連接BM、AF、DA、DM,延長MF交AC于N.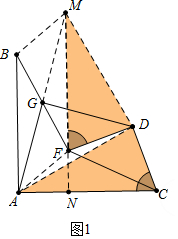
∵BG=GF,AG=GM,
∴四邊形ABMF是平行四邊形,
∴AB=MF=AC,AB∥MN,
∴∠MNC=∠BAC=90°,
∴∠FNC+∠FDC=180°,
∴∠DFN+∠NCD=180°,∵∠MFD+∠DFN=180°,
∴∠MFD=∠ACD,
在△ACD和△MFD中,
$\left\{\begin{array}{l}{AC=MF}\\{∠ACD=∠MFD}\\{CD=DF}\end{array}\right.$,
∴△ACD≌△MFD,
∴DM=AD,∠ADC=∠MDF,
∴∠MDA=∠FDC=90°,
∴△ADM是等腰直角三角形,∵AG=GM,
∴AG⊥DG AG=DG.
(2)如圖2中,過點(diǎn)A作AM⊥AD交DG的延長線于M,連接MB延長MB交CD的延長線于N,連接MF、BD、AF、AD.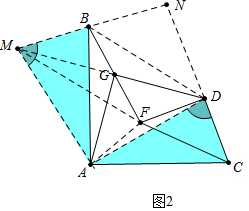
∵∠MAD=90°,∠ADM=45°,
∴∠AMD=∠ADM=45°,
∴AM=AD,
∵∠AMD=∠BAC,
∴∠MAB=∠CAD,∵AM=AD,AB=AC,
∴△MAB≌△DAC,
∴BM=CD=DF,∠AMB=∠ADC,
∵∠ADC+∠ADN=180°,
∴∠AMB+∠ADN=180°,
∴∠MAD+∠N=180°,
∴∠N=∠FDC=90°,
∴NM∥DF,
∴四邊形BDFM是平行四邊形,
∴BG=FG.
點(diǎn)評 本題考查全等三角形的判定和性質(zhì)、等腰直角三角形的性質(zhì)和判定、平行四邊形的判定和性質(zhì)等知識,解題的關(guān)鍵是學(xué)會添加常用輔助線,構(gòu)造特殊四邊形或全等三角形解決問題,題目比較難,輔助線比較多.


 導(dǎo)學(xué)與測試系列答案
導(dǎo)學(xué)與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 4.65×109 | B. | 4.65×1010 | C. | 4.65×1011 | D. | 4.65×1012 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
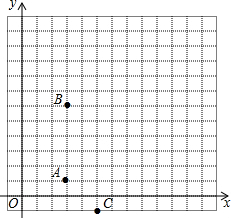 某城市的街道恰好呈東西與南北橫縱交錯格局(如圖所示),一次,警察局電子監(jiān)控器屏幕上發(fā)現(xiàn)一輛作案后的小轎車正在點(diǎn)A(3,1)處以每分鐘0.5個單位長度的速度向北逃竄,根據(jù)各街道的交通狀況進(jìn)行分析,逃犯很可能逃到點(diǎn)B(3,6)后改為向東逃竄,此時正在點(diǎn)C(5,-1)處巡邏的警車接到指令后立即以每分鐘0.7個單位長度的速度進(jìn)行追捕,逃犯將在什么地方被追捕到?
某城市的街道恰好呈東西與南北橫縱交錯格局(如圖所示),一次,警察局電子監(jiān)控器屏幕上發(fā)現(xiàn)一輛作案后的小轎車正在點(diǎn)A(3,1)處以每分鐘0.5個單位長度的速度向北逃竄,根據(jù)各街道的交通狀況進(jìn)行分析,逃犯很可能逃到點(diǎn)B(3,6)后改為向東逃竄,此時正在點(diǎn)C(5,-1)處巡邏的警車接到指令后立即以每分鐘0.7個單位長度的速度進(jìn)行追捕,逃犯將在什么地方被追捕到?查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
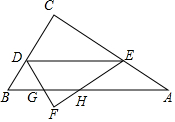 直角三角形ABC中,∠C=90度,CB=6,AC=8,D為CB邊上一個動點(diǎn),E為AC上一點(diǎn),DE∥AB,將三角形CDE沿著DE翻折得到三角形DEF,設(shè)三角形DEF和三角形ABC重合的面積為y,DC=x,求y與x的函數(shù)關(guān)系式及定義域.
直角三角形ABC中,∠C=90度,CB=6,AC=8,D為CB邊上一個動點(diǎn),E為AC上一點(diǎn),DE∥AB,將三角形CDE沿著DE翻折得到三角形DEF,設(shè)三角形DEF和三角形ABC重合的面積為y,DC=x,求y與x的函數(shù)關(guān)系式及定義域.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
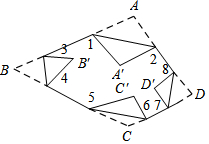 如圖所示,把一個四邊形紙片ABCD的四個頂角分別向內(nèi)折疊,折疊之后,4個頂點(diǎn)不重合,那么圖中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度數(shù)是720°.
如圖所示,把一個四邊形紙片ABCD的四個頂角分別向內(nèi)折疊,折疊之后,4個頂點(diǎn)不重合,那么圖中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度數(shù)是720°.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com