
 如圖,在正方形ABCD中,△BPC是等邊三角形,BP、CP的延長線分別交AD于點E、F,連結BD、DP.下列結論:
如圖,在正方形ABCD中,△BPC是等邊三角形,BP、CP的延長線分別交AD于點E、F,連結BD、DP.下列結論:分析 根據等邊三角形的性質和正方形的性質,得到∠ABE=∠DCF,∠A=∠ADC,AB=CD,證得△ABE≌△DCF,即可判斷①;根據CP=CD和∠DCP=30°即可求出∠CPD,即可判斷②;設正方形邊長為4,求出DF和AE,求出EF,即可判斷③;根據三角形面積計算公式,結合圖形得到△BPD的面積=△BCP的面積+△CDP面積-△BCD的面積,再求出比,即可判斷④.
解答 解:∵△BPC是等邊三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
在△ABE與△CDF中,
$\left\{\begin{array}{l}{∠A=∠ADC}\\{∠ABE=∠DCF}\\{AB=CD}\end{array}\right.$,
∴△ABE≌△DCF,故①正確;
∵PC=CD,∠PCD=30°,
∴∠PDC=75°,∴②正確;
∵四邊形ABCD是正方形,
∴AB=BC=CD=AD,∠ADC=90°,
設AB=BC=CD=AD=4,
∵∠DCF=30°,
∴CF=2DF,DF=$\frac{4}{\sqrt{3}}$=$\frac{4\sqrt{3}}{3}$,CF=$\frac{8\sqrt{3}}{4}$,
同理AE=$\frac{4\sqrt{3}}{3}$,
則AE+DF-EF=AD,
∴EF=$\frac{4\sqrt{3}}{3}$+$\frac{4\sqrt{3}}{3}$-4=$\frac{8\sqrt{3}}{3}$-4,
∵四邊形ABCD是正方形,
∴AD∥BC,
∴$\frac{EF}{AD}$=$\frac{EF}{BC}$=$\frac{\frac{8\sqrt{3}}{3}-4}{4}$=$\frac{\sqrt{3}-1}{3}$,∴③錯誤;
過P作PN⊥BC于N,PM⊥CD于M,
設正方形ABCD的邊長是4,△BPC為正三角形,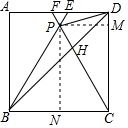
∴∠PBC=∠PCB=60°,PB=PC=BC=CD=4,
∴∠PCD=30°
∴PN=PB•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,PM=PC•sin30°=2,
S△BPD=S四邊形PBCD-S△BCD=S△PBC+S△PDC-S△BCD=$\frac{1}{2}$×4×2$\sqrt{3}$+$\frac{1}{2}$×2×4-$\frac{1}{2}$×4×4=4$\sqrt{3}$-4,
∴$\frac{{S}_{△BPD}}{{S}_{正方形ABCD}}$=$\frac{4\sqrt{3}-4}{4×4}$=$\frac{\sqrt{3}-1}{4}$,∴④正確;
故答案為:①②④.
點評 本題考查的正方形的性質以及等積變換,解答此題的關鍵是作出輔助線,利用銳角三角函數的定義求出PE及PF的長,再根據三角形的面積公式得出結論.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
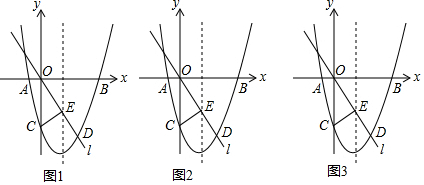
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
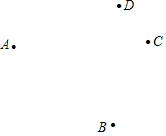 已知平面上A,B,C,D四個點,按下列要求畫出圖形.
已知平面上A,B,C,D四個點,按下列要求畫出圖形.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 4.65×109 | B. | 4.65×1010 | C. | 4.65×1011 | D. | 4.65×1012 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
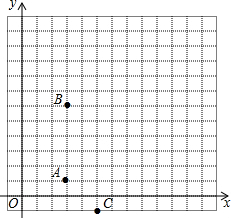 某城市的街道恰好呈東西與南北橫縱交錯格局(如圖所示),一次,警察局電子監控器屏幕上發現一輛作案后的小轎車正在點A(3,1)處以每分鐘0.5個單位長度的速度向北逃竄,根據各街道的交通狀況進行分析,逃犯很可能逃到點B(3,6)后改為向東逃竄,此時正在點C(5,-1)處巡邏的警車接到指令后立即以每分鐘0.7個單位長度的速度進行追捕,逃犯將在什么地方被追捕到?
某城市的街道恰好呈東西與南北橫縱交錯格局(如圖所示),一次,警察局電子監控器屏幕上發現一輛作案后的小轎車正在點A(3,1)處以每分鐘0.5個單位長度的速度向北逃竄,根據各街道的交通狀況進行分析,逃犯很可能逃到點B(3,6)后改為向東逃竄,此時正在點C(5,-1)處巡邏的警車接到指令后立即以每分鐘0.7個單位長度的速度進行追捕,逃犯將在什么地方被追捕到?查看答案和解析>>
科目:初中數學 來源: 題型:填空題
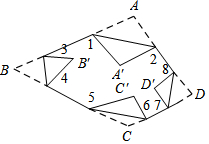 如圖所示,把一個四邊形紙片ABCD的四個頂角分別向內折疊,折疊之后,4個頂點不重合,那么圖中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度數是720°.
如圖所示,把一個四邊形紙片ABCD的四個頂角分別向內折疊,折疊之后,4個頂點不重合,那么圖中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度數是720°.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com