
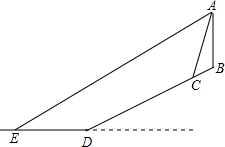
 中考結束后,小明和好朋友一起前往三亞旅游.他們租住的賓館AB坐落在坡度為i=1:2.4的斜坡上.某天,小明在賓館頂樓的海景房A處向外看風景,發現賓館前的 一座雕像C的俯角為76°(雕像的高度忽略不計),遠處海面上一艘即將靠岸的輪船E的俯角為27°.已知雕像C距離海岸線D的距離CD為260米,與賓館AB的水平距離為36米,問此時輪船E距離海岸線D的距離ED的長為( )(參考數據:tan76°≈4.0,tan27°≈0.5,sin76°≈0.97,sin27°≈0.45.
中考結束后,小明和好朋友一起前往三亞旅游.他們租住的賓館AB坐落在坡度為i=1:2.4的斜坡上.某天,小明在賓館頂樓的海景房A處向外看風景,發現賓館前的 一座雕像C的俯角為76°(雕像的高度忽略不計),遠處海面上一艘即將靠岸的輪船E的俯角為27°.已知雕像C距離海岸線D的距離CD為260米,與賓館AB的水平距離為36米,問此時輪船E距離海岸線D的距離ED的長為( )(參考數據:tan76°≈4.0,tan27°≈0.5,sin76°≈0.97,sin27°≈0.45.| A. | 262 | B. | 212 | C. | 244 | D. | 276 |
分析 作AB⊥ED交ED的延長線于H,作CG⊥AB交AB的延長線于G,根據坡度的概念求出BG,根據勾股定理求出BC,得到BD,根據平行線的性質分別求出DH、BH,根據正切的概念計算即可.
解答 解: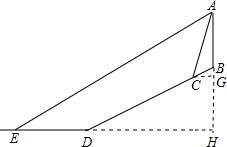 作AB⊥ED交ED的延長線于H,作CG⊥AB交AB的延長線于G,
作AB⊥ED交ED的延長線于H,作CG⊥AB交AB的延長線于G,
∵賓館AB坐落在坡度為i=1:2.4的斜坡上,CG=36米,
∴BG=$\frac{36}{2.4}$=15米,
由勾股定理得,BC=$\sqrt{C{G}^{2}+B{G}^{2}}$=39米,
∴BD=CD+BC=299米,
∵CG∥DH,
∴$\frac{CG}{DH}$=$\frac{BG}{BH}$=$\frac{BC}{BD}$,即$\frac{36}{DH}$=$\frac{15}{BH}$=$\frac{39}{299}$,
解得,DH=276,BH=115,
由題意得,∠ACG=76°,
則tan∠ACG=$\frac{AG}{CG}$,
則AG=36×4=144,
∴AH=AG+BH-BG=244米,
則EH=$\frac{AH}{tan∠E}$=$\frac{244}{0.5}$=488,
∴ED=EH-DH=488-276=212米,
故選:B.
點評 本題考查的是解直角三角形的應用-仰角俯角問題、坡度坡角問題,掌握坡度的概念、仰角俯角的概念、熟記銳角三角函數的定義是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 在所有連結兩點的線中,直線最短 | |
| B. | ∠AOB與∠BOA表示相同的角 | |
| C. | 一個銳角與一個鈍角的和是一個平角 | |
| D. | 兩點之間的線段是兩點之間的距離 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 用一個平面去截一個正方體可能截得五邊形 | |
| B. | 五棱柱有10個頂點 | |
| C. | 沿直角三角形某條邊所在的直線旋轉一周,所得的幾何體為圓柱 | |
| D. | 將折起的扇子打開,屬于“線動成面”的現象 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
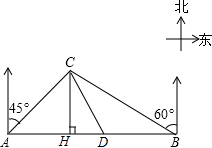 川西某高原上有一條筆直的公路,在緊靠公路相距40千米的A、B兩地,分別有甲、乙兩個醫療站,如圖,在A地北偏東45°,B地北偏西60°方向上有一牧民區C,過點C作CH⊥AB于H.
川西某高原上有一條筆直的公路,在緊靠公路相距40千米的A、B兩地,分別有甲、乙兩個醫療站,如圖,在A地北偏東45°,B地北偏西60°方向上有一牧民區C,過點C作CH⊥AB于H.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖是一個平面直角坐標系,已知點A,B,C,D的坐標分別為(-2,-3),(2,-2),(3,1),(-4,5)按要求完成下列各小題.
如圖是一個平面直角坐標系,已知點A,B,C,D的坐標分別為(-2,-3),(2,-2),(3,1),(-4,5)按要求完成下列各小題.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com