
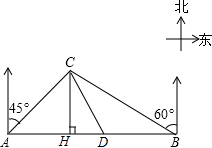
 川西某高原上有一條筆直的公路,在緊靠公路相距40千米的A、B兩地,分別有甲、乙兩個(gè)醫(yī)療站,如圖,在A地北偏東45°,B地北偏西60°方向上有一牧民區(qū)C,過(guò)點(diǎn)C作CH⊥AB于H.
川西某高原上有一條筆直的公路,在緊靠公路相距40千米的A、B兩地,分別有甲、乙兩個(gè)醫(yī)療站,如圖,在A地北偏東45°,B地北偏西60°方向上有一牧民區(qū)C,過(guò)點(diǎn)C作CH⊥AB于H.分析 (1)設(shè)CH=x,分別表示出AH,BH的值,讓其相加得40求值即可求得CH的長(zhǎng),進(jìn)而可求得CB的長(zhǎng);
(2)由CD和BC的數(shù)量關(guān)系可得CD和CH的數(shù)量關(guān)系,根據(jù)特殊角的三角函數(shù)值可求出∠ADC的度數(shù),進(jìn)而可得HD的長(zhǎng),用BH的長(zhǎng)減去DH的長(zhǎng)即為BD的距離.
解答 解:(1)設(shè)CH為x千米,由題意得,∠CBH=30°,∠CAH=45°,
∴AH=CH=x,
在Rt△BCH中,tan30°=$\frac{x}{BH}$=$\frac{\sqrt{3}}{3}$,
∴BH=$\sqrt{3}$x,
∵AH+HB=AB=40,
∴x+$\sqrt{3}$x=40,
解得x=20$\sqrt{3}$-20,
∴CB=2CH=40$\sqrt{3}$-40.
答:牧民區(qū)C到B地的距離為(40$\sqrt{3}$-40)千米;
(2)∵C、D 兩地距離是B、C兩地距離的$\frac{\sqrt{3}}{3}$倍,CH=$\frac{1}{2}$BC,
∴sin∠ADC=$\frac{CH}{CD}$=$\frac{\frac{1}{2}BC}{\frac{\sqrt{3}}{3}BC}$=$\frac{\sqrt{3}}{2}$,
∴∠ADC=60°.
在Rt△CHD中,DH=CH•cot∠CDH=$\frac{\sqrt{3}}{3}$CH,
∵BH=$\sqrt{3}$CH,CH=20$\sqrt{3}$-20,
∴BD=BH-DH=$\sqrt{3}$CH-$\frac{\sqrt{3}}{3}$CH=$\frac{2\sqrt{3}}{3}$(20$\sqrt{3}$-20)=40-$\frac{40\sqrt{3}}{3}$.
答:BD之間的距離為40-$\frac{40\sqrt{3}}{3}$千米.
點(diǎn)評(píng) 本題考查了解直角三角形的應(yīng)用以及構(gòu)造直角三角形,利用勾股定理及特殊的三角函數(shù)值求解是解決本題關(guān)鍵.


 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
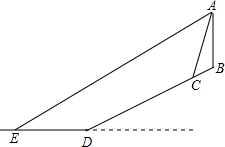 中考結(jié)束后,小明和好朋友一起前往三亞旅游.他們租住的賓館AB坐落在坡度為i=1:2.4的斜坡上.某天,小明在賓館頂樓的海景房A處向外看風(fēng)景,發(fā)現(xiàn)賓館前的 一座雕像C的俯角為76°(雕像的高度忽略不計(jì)),遠(yuǎn)處海面上一艘即將靠岸的輪船E的俯角為27°.已知雕像C距離海岸線D的距離CD為260米,與賓館AB的水平距離為36米,問(wèn)此時(shí)輪船E距離海岸線D的距離ED的長(zhǎng)為( )(參考數(shù)據(jù):tan76°≈4.0,tan27°≈0.5,sin76°≈0.97,sin27°≈0.45.
中考結(jié)束后,小明和好朋友一起前往三亞旅游.他們租住的賓館AB坐落在坡度為i=1:2.4的斜坡上.某天,小明在賓館頂樓的海景房A處向外看風(fēng)景,發(fā)現(xiàn)賓館前的 一座雕像C的俯角為76°(雕像的高度忽略不計(jì)),遠(yuǎn)處海面上一艘即將靠岸的輪船E的俯角為27°.已知雕像C距離海岸線D的距離CD為260米,與賓館AB的水平距離為36米,問(wèn)此時(shí)輪船E距離海岸線D的距離ED的長(zhǎng)為( )(參考數(shù)據(jù):tan76°≈4.0,tan27°≈0.5,sin76°≈0.97,sin27°≈0.45.| A. | 262 | B. | 212 | C. | 244 | D. | 276 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
 如圖,線段AB邊長(zhǎng)為1個(gè)單位長(zhǎng)度的正方形分割為兩個(gè)等腰直角三角形,以A為圓心,AB的長(zhǎng)為半徑畫(huà)弧交數(shù)軸于點(diǎn)C,那么點(diǎn)C在數(shù)軸上表示的實(shí)數(shù)是( )
如圖,線段AB邊長(zhǎng)為1個(gè)單位長(zhǎng)度的正方形分割為兩個(gè)等腰直角三角形,以A為圓心,AB的長(zhǎng)為半徑畫(huà)弧交數(shù)軸于點(diǎn)C,那么點(diǎn)C在數(shù)軸上表示的實(shí)數(shù)是( )| A. | 1+$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{2}-1$ | D. | 1 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $m>\frac{1}{2}$ | B. | m<1 | C. | $m<-\frac{1}{2}$或m>1 | D. | $-\frac{1}{2}<m<1$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
 先閱讀理解下面的例題,再按要求解答下列問(wèn)題:
先閱讀理解下面的例題,再按要求解答下列問(wèn)題:查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com