
 如圖,A、B兩城市相距80km,現計劃在這兩座城市間修建一條高速公路(即線段AB),經測量,森林保護中心P在A城市的北偏東30°和B城市的北偏西45°的方向上,已知森林保護區的范圍在以P點為圓心,50km為半徑的圓形區域內,請問計劃修建的這條高速公路會不會穿越保護區,為什么?(參考數據:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如圖,A、B兩城市相距80km,現計劃在這兩座城市間修建一條高速公路(即線段AB),經測量,森林保護中心P在A城市的北偏東30°和B城市的北偏西45°的方向上,已知森林保護區的范圍在以P點為圓心,50km為半徑的圓形區域內,請問計劃修建的這條高速公路會不會穿越保護區,為什么?(參考數據:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414) 分析 過點P作PM⊥AB,M是垂足.AM與BM就都可以根據三角函數用PPM表示出來.根據AB的長,得到一個關于PM的方程,解出PM的長.從而判斷出這條高速公路會不會穿越保護區.
解答 解:作PM⊥AB,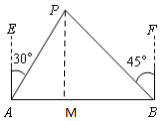
由題意得:AE∥PM∥BF,
∴∠APM=30°,∠BPM=45°,
∴PM=$\frac{AM}{tan∠APM}$=$\sqrt{3}$AM,BM=PM,
設BM=PM=x,則AM=$\frac{\sqrt{3}}{3}$x,
∴$\frac{{\sqrt{3}}}{3}x+x=80$
∴x=120-40$\sqrt{3}$≈50.72>50,
∴這條高速公路不會穿越保護區.
點評 本題主要考查解直角三角形的應用,解一般三角形的問題一般可以轉化為解直角三角形的問題,解決的方法就是作高線.


 智能訓練練測考系列答案
智能訓練練測考系列答案 計算高手系列答案
計算高手系列答案科目:初中數學 來源: 題型:選擇題
 如圖,在平面直角坐標系中,⊙A經過原點O,并且分別與x軸、y軸交于B、C兩點,已知B(8,0),C(0,6),則⊙A的半徑為( )
如圖,在平面直角坐標系中,⊙A經過原點O,并且分別與x軸、y軸交于B、C兩點,已知B(8,0),C(0,6),則⊙A的半徑為( )| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,數軸上表示1、$\sqrt{2}$的對應點分別為A、B,點C為點B關于點A的對稱點,設點C所表示的數為x.
如圖,數軸上表示1、$\sqrt{2}$的對應點分別為A、B,點C為點B關于點A的對稱點,設點C所表示的數為x.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
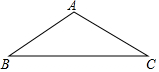 如圖,某廠房人字架屋頂的上弦AB=AC=10米,∠β=α,則該屋頂的跨度BC為( )
如圖,某廠房人字架屋頂的上弦AB=AC=10米,∠β=α,則該屋頂的跨度BC為( )| A. | 10sinα米 | B. | 10cosα米 | C. | 20sinα米 | D. | 20cosα米 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知⊙O過邊長為4的正方形ABCD頂點A、B.
如圖,已知⊙O過邊長為4的正方形ABCD頂點A、B.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com