
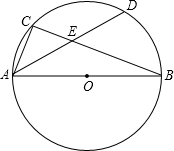
 如圖,AB為⊙O的直徑,C為⊙O上一點,弦AD平分∠BAC,交BC于點E,AB=10,AD=8,則AE的長為$\frac{7}{2}$.
如圖,AB為⊙O的直徑,C為⊙O上一點,弦AD平分∠BAC,交BC于點E,AB=10,AD=8,則AE的長為$\frac{7}{2}$. 分析 連接BD、CD,由勾股定理先求出BD的長,再利用△ABD∽△BED,得出$\frac{DE}{DB}=\frac{DB}{AD}$,可解得DE的長,由AE=AD-DE求解即可得出答案.
解答 解:連接BD、CD,如圖所示,
∵AB為⊙O的直徑,
∴∠ADB=90°,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∵弦AD平分∠BAC,
∴CD=BD=6,
∴∠CBD=∠DAB,
∴△ABD∽△BED,
∴$\frac{DE}{DB}=\frac{DB}{AD}$,即$\frac{DE}{6}=\frac{6}{8}$,
解得DE=$\frac{9}{2}$,
∴AE=AD-DE=8-$\frac{9}{2}$=$\frac{7}{2}$;
故答案為:$\frac{7}{2}$.
點評 此題主要考查了三角形相似的判定和性質及圓周角定理,解答此題的關鍵是得出△ABD∽△BED.


 優百分課時互動系列答案
優百分課時互動系列答案 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案科目:初中數學 來源: 題型:選擇題
 如圖,在等腰Rt△ABC中,AB=BC;AD平分∠BAC交BC邊于點D,點E是AD邊上靠近端點A的一動點,以AE為邊往上作等腰Rt△AEF,且AE=EF,延長FE交AC于點G;點M為FC中點,連接BM、EM、BE、DM;則下列5個結論:①FA=FG;②△ABD與△ACD的面積比為1:$\sqrt{2}$;③AC=($\sqrt{2}$+1)BD;④∠MDC=90°;⑤△BME為等腰三角形,但不一定為直角三角形,其中正確的有( )個.
如圖,在等腰Rt△ABC中,AB=BC;AD平分∠BAC交BC邊于點D,點E是AD邊上靠近端點A的一動點,以AE為邊往上作等腰Rt△AEF,且AE=EF,延長FE交AC于點G;點M為FC中點,連接BM、EM、BE、DM;則下列5個結論:①FA=FG;②△ABD與△ACD的面積比為1:$\sqrt{2}$;③AC=($\sqrt{2}$+1)BD;④∠MDC=90°;⑤△BME為等腰三角形,但不一定為直角三角形,其中正確的有( )個.| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 在平面直角坐標系中,⊙P的圓心P的坐標為(a,4),半徑為2,函數y=x的圖象被⊙P截得的弦AB的長為$2\sqrt{3}$,則a的值為4-$\sqrt{2}$或4+$\sqrt{2}$.
在平面直角坐標系中,⊙P的圓心P的坐標為(a,4),半徑為2,函數y=x的圖象被⊙P截得的弦AB的長為$2\sqrt{3}$,則a的值為4-$\sqrt{2}$或4+$\sqrt{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 甲數的3倍與乙數的$\frac{1}{2}$的和 | B. | a與1的差的$\frac{1}{4}$ | ||
| C. | 一個數的2倍比3小1 | D. | a與b的和的$\frac{3}{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖所示,將矩形ABCD分成15個大小相等的正方形,E、F、G、H分別在AD、AB、BC、CD邊上,且是某個小正方形的頂點.若四邊形EFGH的面積為1,則矩形ABCD的面積是( )
如圖所示,將矩形ABCD分成15個大小相等的正方形,E、F、G、H分別在AD、AB、BC、CD邊上,且是某個小正方形的頂點.若四邊形EFGH的面積為1,則矩形ABCD的面積是( )| A. | $\frac{5}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{15}{8}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,A、B兩城市相距80km,現計劃在這兩座城市間修建一條高速公路(即線段AB),經測量,森林保護中心P在A城市的北偏東30°和B城市的北偏西45°的方向上,已知森林保護區的范圍在以P點為圓心,50km為半徑的圓形區域內,請問計劃修建的這條高速公路會不會穿越保護區,為什么?(參考數據:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
如圖,A、B兩城市相距80km,現計劃在這兩座城市間修建一條高速公路(即線段AB),經測量,森林保護中心P在A城市的北偏東30°和B城市的北偏西45°的方向上,已知森林保護區的范圍在以P點為圓心,50km為半徑的圓形區域內,請問計劃修建的這條高速公路會不會穿越保護區,為什么?(參考數據:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com