
 如圖,在等腰Rt△ABC中,AB=BC;AD平分∠BAC交BC邊于點D,點E是AD邊上靠近端點A的一動點,以AE為邊往上作等腰Rt△AEF,且AE=EF,延長FE交AC于點G;點M為FC中點,連接BM、EM、BE、DM;則下列5個結(jié)論:①FA=FG;②△ABD與△ACD的面積比為1:$\sqrt{2}$;③AC=($\sqrt{2}$+1)BD;④∠MDC=90°;⑤△BME為等腰三角形,但不一定為直角三角形,其中正確的有( )個.
如圖,在等腰Rt△ABC中,AB=BC;AD平分∠BAC交BC邊于點D,點E是AD邊上靠近端點A的一動點,以AE為邊往上作等腰Rt△AEF,且AE=EF,延長FE交AC于點G;點M為FC中點,連接BM、EM、BE、DM;則下列5個結(jié)論:①FA=FG;②△ABD與△ACD的面積比為1:$\sqrt{2}$;③AC=($\sqrt{2}$+1)BD;④∠MDC=90°;⑤△BME為等腰三角形,但不一定為直角三角形,其中正確的有( )個.| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 ①正確.只要證明∠FAG=∠FGA=67.5°即可.
②正確.作DN⊥AC于N,因為DA平分∠BAC,∠DAB=∠DAC,所以DB=DN,故$\frac{{S}_{△ABD}}{{S}_{△ADC}}$=$\frac{\frac{1}{2}•AB•DB}{\frac{1}{2}•AC•DN}$=$\frac{AB}{AC}$=$\frac{1}{\sqrt{2}}$.
③錯誤.由△ADN≌△ADB,可知AN=AB=BC,所以DC=$\sqrt{2}$DN=$\sqrt{2}$BD,所以AC=AN+CN=BC+BD=2BD+$\sqrt{2}$BD=(2+$\sqrt{2}$)BD.
④錯誤.觀察圖2,即可解決問題.
⑤錯誤.如圖1中,延長EM到H,使得MH=EM,連接BH、CH延長AD交CH的延長線于K.先證明△MFE≌△MCH,再證明△BAE≌△BCH,即可證明△EBM是等腰直角三角形.
解答 解:如圖1中,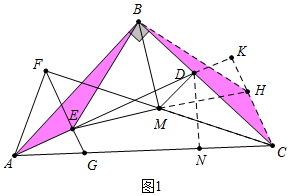
∵BA=BC,∠ABC=90°,
∴∠BAC=∠BCA=45°,AC=$\sqrt{2}$AB,
∵AD平分∠BAC,
∴∠DAB=∠DAC=22.5°,
∵EA=EF,∠AEF=90°,
∴∠EAF=∠EFA=45°,
∴FAG=67.5°,∠FGA=180°-∠FAG-∠AFE=67.5°,
∴∠FAG=∠FGA,
∴FA=FG,故①正確,
作DN⊥AC于N,
∵DA平分∠BAC,∠DAB=∠DAC,
∴DB=DN,
∴$\frac{{S}_{△ABD}}{{S}_{△ADC}}$=$\frac{\frac{1}{2}•AB•DB}{\frac{1}{2}•AC•DN}$=$\frac{AB}{AC}$=$\frac{1}{\sqrt{2}}$,故②正確,
由△ADN≌△ADB,可知AN=AB=BC,
∴DC=$\sqrt{2}$DN=$\sqrt{2}$BD,
∴AC=AN+CN=BC+BD=2BD+$\sqrt{2}$BD=(2+$\sqrt{2}$)BD,故③錯誤,
如圖2中,當點M在線段AD上時,∠MDC=∠ABD+∠BAD>90°,故④錯誤.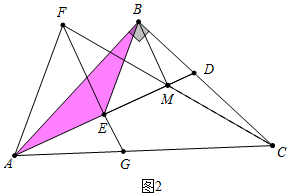
如圖1中,延長EM到H,使得MH=EM,連接BH、CH延長AD交CH的延長線于K.
在△MFE和△MCH中,
$\left\{\begin{array}{l}{MF=MC}\\{∠FME=∠CMH}\\{EM=MH}\end{array}\right.$,
∴△MFE≌△MCH,
∴CH=EF=AE,∠MFE=∠MCH,
∴EF∥CK,
∴∠FED=∠K=90°,
∵∠BAE+∠ADB=90°,∠BCH+∠CDK=90°,∠ADB=∠CDK,
∴∠BAE=∠BCH,
在△BAE和△BCH中,
$\left\{\begin{array}{l}{BA=BC}\\{∠BAE=∠BCH}\\{AE=CH}\end{array}\right.$,
∴△BAE≌△BCH,
∴BE=BH,∠ABE=∠CBH,
∴∠EBH=∠ABC=90°,∵EM=MH,
∴BM⊥EM,BM=$\frac{1}{2}$EH=EM,
∴△EBM是等腰直角三角形,故⑤錯誤.
故選A.
點評 本題考查全等三角形的判定和性質(zhì)、等腰直角三角形的性質(zhì)、角平分線的性質(zhì)定理、三角形的面積等知識,解題的關(guān)鍵是學(xué)會添加常用輔助線,構(gòu)造全等三角形解決問題,所以中考選擇題中的壓軸題.


科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | m<2 | B. | m>2 | C. | m≤2 | D. | m≥2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
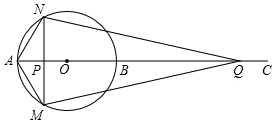 已知:如圖,AB為⊙O的直徑,點C為AB延長線上一點,動點P從點A出發(fā)沿AC方向以1cm/s的速度運動,同時動點Q從點C出發(fā)以相同的速度沿CA方向運動,當兩點相遇時停止運動,過點P作AB的垂線,分別交⊙O于點M和點N,已知⊙O的半徑為2,AC=10,設(shè)運動時間為ts.
已知:如圖,AB為⊙O的直徑,點C為AB延長線上一點,動點P從點A出發(fā)沿AC方向以1cm/s的速度運動,同時動點Q從點C出發(fā)以相同的速度沿CA方向運動,當兩點相遇時停止運動,過點P作AB的垂線,分別交⊙O于點M和點N,已知⊙O的半徑為2,AC=10,設(shè)運動時間為ts.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
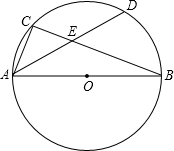 如圖,AB為⊙O的直徑,C為⊙O上一點,弦AD平分∠BAC,交BC于點E,AB=10,AD=8,則AE的長為$\frac{7}{2}$.
如圖,AB為⊙O的直徑,C為⊙O上一點,弦AD平分∠BAC,交BC于點E,AB=10,AD=8,則AE的長為$\frac{7}{2}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,在平面直角坐標系中,⊙A經(jīng)過原點O,并且分別與x軸、y軸交于B、C兩點,已知B(8,0),C(0,6),則⊙A的半徑為( )
如圖,在平面直角坐標系中,⊙A經(jīng)過原點O,并且分別與x軸、y軸交于B、C兩點,已知B(8,0),C(0,6),則⊙A的半徑為( )| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com