
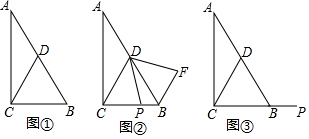
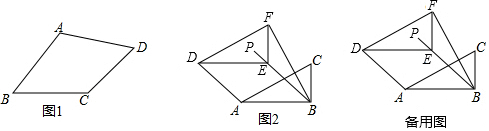
分析 (1)利用含30°的直角三角形的性質(zhì)得出BC=$\frac{1}{2}$AB,即可得出結(jié)論;
(2)同(1)的方法得出BC=BD進(jìn)而得出△BCD是等邊三角形,進(jìn)而判斷出△DCP≌△DBF得出CP=BF即可得出結(jié)論;
(3)同(2)的方法得出結(jié)論.
解答 解:(1)∵∠ACB=90°,∠A=30°,
∴∠CBA=60°,BC=$\frac{1}{2}$AB,
∵點(diǎn)D是AB的中點(diǎn),
∴BC=BD,
故答案為:BC=BD;
(2)BF+BP=BD,
理由:∵∠ACB=90°,∠A=30°,
∴∠CBA=60°,BC=$\frac{1}{2}$AB,
∵點(diǎn)D是AB的中點(diǎn),
∴BC=BD,
∴△DBC是等邊三角形,
∴∠CDB=60°,DC=DB,
∵線段DP繞點(diǎn)D逆時(shí)針旋轉(zhuǎn)60°,得到線段DF,
∴∠PDF=60°,DP=DF,
∴∠CDB-∠PDB=∠PDF-∠PDB,
∴∠CDP=∠BDF,
在△DCP和△DBF中,$\left\{\begin{array}{l}{DC=DB}\\{∠CDP=∠BDF}\\{DP=DF}\end{array}\right.$,
∴△DCP≌△DBF,
∴CP=BF,
∵CP+BP=BC,
∴BF+BP=BC,
∵BC=BD,
∴BF+BP=BD;
(3)如圖③,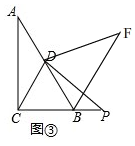 BF=BD+BP,
BF=BD+BP,
理由:∵∠ACB=90°,∠A=30°,
∴∠CBA=60°,BC=$\frac{1}{2}$AB,
∵點(diǎn)D是AB的中點(diǎn),
∴BC=BD,
∴△DBC是等邊三角形,
∴∠CDB=60°,DC=DB,
∵線段DP繞點(diǎn)D逆時(shí)針旋轉(zhuǎn)60°,得到線段DF,
∴∠PDF=60°,DP=DF,
∴∠CDB+∠PDB=∠PDF+∠PDB,
∴∠CDP=∠BDF,
在△DCP和△DBF中,$\left\{\begin{array}{l}{DC=DB}\\{∠CDP=∠BDF}\\{DP=DF}\end{array}\right.$,
∴△DCP≌△DBF,
∴CP=BF,
∵CP=BC+BP,
∴BF=BC+BP,
∵BC=BD,
∴BF=BD+BP.
點(diǎn)評 此題是三角形綜合題,主要考查了含30°的直角三角形的性質(zhì),等邊三角形的判定,全等三角形的判定和性質(zhì),旋轉(zhuǎn)的性質(zhì),解本題的關(guān)鍵是判斷出△DCP≌△DBF,是一道中等難度的中考常考題.


 世紀(jì)百通優(yōu)練測系列答案
世紀(jì)百通優(yōu)練測系列答案 百分學(xué)生作業(yè)本題練王系列答案
百分學(xué)生作業(yè)本題練王系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
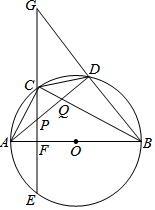 已知:如圖,△ABC內(nèi)接于⊙O,AB為直徑,弦CE⊥AB于F,D是弧BC上的一點(diǎn),CD=AE,連結(jié)BD并延長交EC的延長線于點(diǎn)G,連結(jié)AD,分別交CE、BC于點(diǎn)P、Q.
已知:如圖,△ABC內(nèi)接于⊙O,AB為直徑,弦CE⊥AB于F,D是弧BC上的一點(diǎn),CD=AE,連結(jié)BD并延長交EC的延長線于點(diǎn)G,連結(jié)AD,分別交CE、BC于點(diǎn)P、Q.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
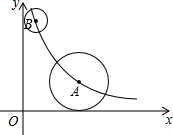 如圖,在平面直角坐標(biāo)系中,點(diǎn)A、B均在函數(shù)y=$\frac{k}{x}$(k>0,x>0)的圖象上,⊙A與x軸相切,⊙B與y軸相切.若點(diǎn)A的坐標(biāo)為(3,2),且⊙A的半徑是⊙B的半徑的2倍,則點(diǎn)B的坐標(biāo)為(1,6).
如圖,在平面直角坐標(biāo)系中,點(diǎn)A、B均在函數(shù)y=$\frac{k}{x}$(k>0,x>0)的圖象上,⊙A與x軸相切,⊙B與y軸相切.若點(diǎn)A的坐標(biāo)為(3,2),且⊙A的半徑是⊙B的半徑的2倍,則點(diǎn)B的坐標(biāo)為(1,6).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
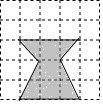 如圖,方格圖中小正方形的邊長為1.將方格圖中陰影部分圖形剪下來,再把剪下的陰影部分重新剪拼成一個(gè)正方形(不重疊無縫隙),那么所拼成的這個(gè)正方形的邊長為$\sqrt{6}$.
如圖,方格圖中小正方形的邊長為1.將方格圖中陰影部分圖形剪下來,再把剪下的陰影部分重新剪拼成一個(gè)正方形(不重疊無縫隙),那么所拼成的這個(gè)正方形的邊長為$\sqrt{6}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
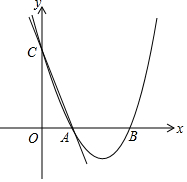 如圖所示,直線AC:y=-2x+2與x軸交于點(diǎn)A,與y軸交于點(diǎn)C,拋物線y=ax2 +bx+c(a>0)過A,C兩點(diǎn),與x軸交于另一點(diǎn)B(B在A的右側(cè)),且△OBC∽△OCA.
如圖所示,直線AC:y=-2x+2與x軸交于點(diǎn)A,與y軸交于點(diǎn)C,拋物線y=ax2 +bx+c(a>0)過A,C兩點(diǎn),與x軸交于另一點(diǎn)B(B在A的右側(cè)),且△OBC∽△OCA.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com