
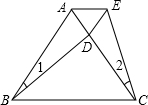
 如圖,△ABC是等邊三角形,D為AC邊上的一點,且∠1=∠2,BD=CE.
如圖,△ABC是等邊三角形,D為AC邊上的一點,且∠1=∠2,BD=CE.分析 (1)△ABD和△ACE是全等三角形,利用SAS即可證明;
(2)根據△ABD≌△ACE得到AD=AE,∠CAE=∠BAD,即可判定出△ADE的形狀.
解答 解:(1)∵△ABC是等邊三角形,
∴AB=AC,∠BAC=60°,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠1=∠2}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△ACE(SAS);
(2)△ADE是等邊三角形
理由:∵△ABD≌△ACE,
∴AD=AE,∠CAE=∠BAD=60°,
∴△ADE是等邊三角形.
點評 此題考查了等邊三角形的判定與性質以及全等三角形的判定與性質.解題要掌握SAS證明三角形全等,此題難度不大,注意掌握數形結合思想的應用.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
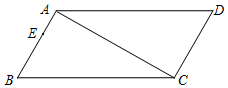
 已知如圖,AC=AE,AD=AB,∠ACB=∠DAB=90°,AE∥CB,AC、DE交于點F.
已知如圖,AC=AE,AD=AB,∠ACB=∠DAB=90°,AE∥CB,AC、DE交于點F.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
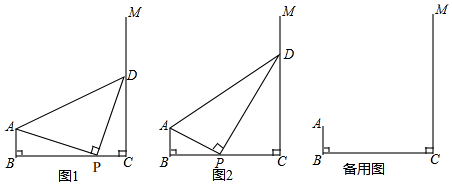
科目:初中數學 來源: 題型:解答題
 如圖,在四邊形ABCD中,∠B=∠D=60°,∠BAC=∠ACD=90°,點E為邊AB上一點,AB=3AE=3cm,動點P從B點出發,以1cm/s的速度沿BC→CD→DA運動至A點停止,設運動時間為t秒.
如圖,在四邊形ABCD中,∠B=∠D=60°,∠BAC=∠ACD=90°,點E為邊AB上一點,AB=3AE=3cm,動點P從B點出發,以1cm/s的速度沿BC→CD→DA運動至A點停止,設運動時間為t秒.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
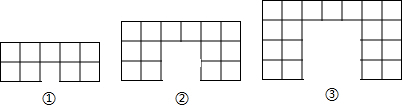
| 圖形個數(n) | ① | ② | ③ |
| 正方形的個數 | 9 | 13 | 18 |
| 圖形的周長 | 16 | 28 | 38 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
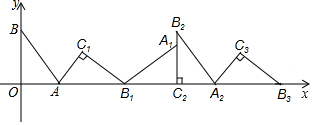
| A. | (18,0) | B. | (18,2) | C. | (16,2) | D. | (16,0) |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,用一個半徑為30cm扇形鐵皮,制作一個無底的圓錐(不計損耗),經測量圓錐的底面半徑r為10cm,則扇形鐵皮的面積為300πcm2.(結果保留π)
如圖,用一個半徑為30cm扇形鐵皮,制作一個無底的圓錐(不計損耗),經測量圓錐的底面半徑r為10cm,則扇形鐵皮的面積為300πcm2.(結果保留π)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com