
分析 根據勾股定理的逆定理可知,當三角形中三邊的關系為:a2+b2=c2時,則三角形為直角三角形.
解答 解:(1)52+122=132,符合勾股定理的逆定理,能組成直角三角形;
(2)122+162=202,符合勾股定理的逆定理,能組成直角三角形;
(3)52+62≠82,不符合勾股定理的逆定理,不能組成直角三角;
(4)$\sqrt{2}$2+$\sqrt{7}$2=32,符合勾股定理的逆定理,能組成直角三角形;
(5)$\sqrt{7}$2+$\sqrt{15}$2=$\sqrt{22}$2,符合勾股定理的逆定理,能組成直角三角形;
故答案為:是直角三角形;是直角三角形;不是直角三角形;是直角三角形;是直角三角形.
點評 此題考查的知識點是勾股數,解答此題要用到勾股定理的逆定理:已知三角形ABC的三邊滿足:a2+b2=c2時,則三角形ABC是直角三角形.解答時,只需看兩較小數的平方和是否等于最大數的平方.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案 目標測試系列答案
目標測試系列答案科目:初中數學 來源: 題型:解答題
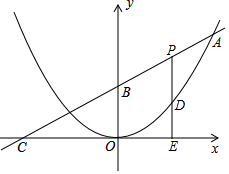 如圖,已知二次函數圖象的頂點在原點,直線y=$\frac{1}{2}$x+4的圖象與該二次函數的圖象交于點A(m,8),直線與x軸的交點為C,與y軸的交點為B.
如圖,已知二次函數圖象的頂點在原點,直線y=$\frac{1}{2}$x+4的圖象與該二次函數的圖象交于點A(m,8),直線與x軸的交點為C,與y軸的交點為B.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
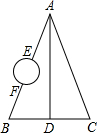 如圖,A,B,C,D是四個村莊,B,D,C在一條東西走向公路的沿線上,BD=DC=l km,村莊AC,AD間也有公路相連,且公路AD是南北走向,AC=3km,只有AB之間由于間隔了一個小湖,所以無直接相連的公路.現決定在湖面上造一座斜拉橋,測得AE=1.2km,BF=0.7km,則建造的斜拉橋長至少為1.1km.
如圖,A,B,C,D是四個村莊,B,D,C在一條東西走向公路的沿線上,BD=DC=l km,村莊AC,AD間也有公路相連,且公路AD是南北走向,AC=3km,只有AB之間由于間隔了一個小湖,所以無直接相連的公路.現決定在湖面上造一座斜拉橋,測得AE=1.2km,BF=0.7km,則建造的斜拉橋長至少為1.1km.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
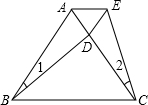 如圖,△ABC是等邊三角形,D為AC邊上的一點,且∠1=∠2,BD=CE.
如圖,△ABC是等邊三角形,D為AC邊上的一點,且∠1=∠2,BD=CE.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com