
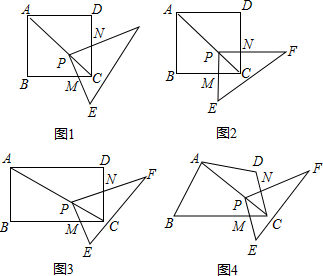
分析 (1)①先判定△PMC∽△ABC,再根據相似三角形的對應邊成比例進行求解;②先用①中的方法求得正方形PMCN的邊長,再計算其面積;
(2)先過P作PG⊥BC于G,作PH⊥CD于H,判定△PGM∽△PHN,再根據相似三角形的性質以及平行線分線段成比例定理進行推導計算即可;
(3)先過P作PG∥AB,作PH∥AD,并結合條件∠B+∠D=180°,判定△PGM∽△PHN,再根據相似三角形的性質以及平行線分線段成比例定理進行推導計算即可.
解答 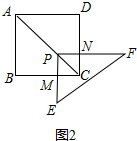 解:(1)①如圖2,∵PM⊥BC,AB⊥BC
解:(1)①如圖2,∵PM⊥BC,AB⊥BC
∴△PMC∽△ABC
∴$\frac{CP}{CA}$=$\frac{PM}{AB}$
又∵AP=2PC
∴$\frac{PM}{AB}$=$\frac{1}{3}$,即$\frac{PM}{a}$=$\frac{1}{3}$
∴PM=$\frac{1}{3}$a,即正方形PMCN的邊長是$\frac{1}{3}$a
②當AP=nPC時(n是正實數),$\frac{PM}{AB}$=$\frac{1}{n+1}$
∴PM=$\frac{1}{n+1}$a
∴四邊形PMCN的面積=($\frac{1}{n+1}$a)2=$\frac{{a}^{2}}{(n+1)^{2}}$
(2)如圖3,過P作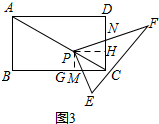 PG⊥BC于G,作PH⊥CD于H,則∠PGM=∠PHN=90°,∠GPH=90°
PG⊥BC于G,作PH⊥CD于H,則∠PGM=∠PHN=90°,∠GPH=90°
∵Rt△PEF中,∠FPE=90°
∴∠GPM=∠HPN
∴△PGM∽△PHN
∴$\frac{PM}{PN}$=$\frac{PG}{PH}$
由PG∥AB,PH∥AD可得,$\frac{PG}{AB}=\frac{CP}{CA}=\frac{PH}{AD}$
∵AB=a,BC=b
∴$\frac{PG}{a}=\frac{PH}{b}$,即$\frac{PG}{PH}$=$\frac{a}{b}$
∴$\frac{PM}{PN}$=$\frac{a}{b}$
(3)如圖4,過P作PG∥AB,交BC于G,作PH∥AD,交CD于H,則∠HPG=∠DAB
∵∠EPF=∠BAD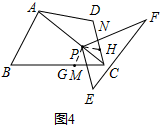
∴∠EPF=∠GPH,即∠EPH+∠HPN=∠EPH+∠GPM
∴∠HPN=∠GPM
∵∠B+∠D=180°
∴∠PGC+∠PHC=180°
又∵∠PHN+∠PHC=180°
∴∠PGC=∠PHN
∴△PGM∽△PHN
∴$\frac{PM}{PN}$=$\frac{PG}{PH}$①
由PG∥AB,PH∥AD可得,$\frac{PG}{AB}$=$\frac{CP}{CA}$=$\frac{PH}{AD}$
即$\frac{PG}{PH}$=$\frac{AB}{AD}$②
∴由①②可得,$\frac{PM}{PN}$=$\frac{AB}{AD}$
點評 本題主要考查了相似三角形的應用以及平行線分線段成比例定理,解決問題的關鍵是作輔助線構造相似三角形,并根據兩角對應相等判定兩個三角形相似.解題時注意,平行于三角形的一邊,并且和其他兩邊相交的直線,所截得的三角形的三邊與原三角形的三邊對應成比例.


 鷹派教輔銜接教材河北教育出版社系列答案
鷹派教輔銜接教材河北教育出版社系列答案 初中暑期銜接系列答案
初中暑期銜接系列答案科目:初中數學 來源: 題型:填空題
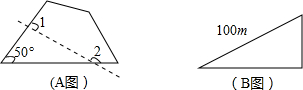 請從以下兩題中任選一題作答,若多選,則按所選的第一題計分.
請從以下兩題中任選一題作答,若多選,則按所選的第一題計分.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
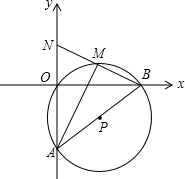 如圖,在平面直角坐標系中,O(0,0),A(0,-6),B(8,0)三點在⊙P上.
如圖,在平面直角坐標系中,O(0,0),A(0,-6),B(8,0)三點在⊙P上.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
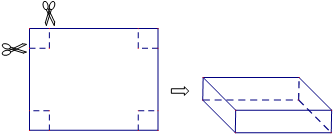
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com