
分析 由于二次函數(shù)的二次項(xiàng)系數(shù)a=1>0,由此可以確定拋物線開口方向,利用y=ax2+bx+c的頂點(diǎn)坐標(biāo)公式為(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),對稱軸是x=-$\frac{b}{2a}$可以確定對稱軸,然后即可確定在對稱軸的左側(cè)y隨x的增大而減小,由此得到x的取值范圍.
解答 解:∵y=x2-2x+3,
∴二次函數(shù)的二次項(xiàng)系數(shù)a=1>0,
∴拋物線開口向上,
∵y=ax2+bx+c的頂點(diǎn)坐標(biāo)公式為(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),對稱軸是x=-$\frac{b}{2a}$,
∴此函數(shù)對稱軸是x=1,頂點(diǎn)坐標(biāo)是(1,2),
∴當(dāng)x<1時(shí),y隨x的增大而減小.
故答案為:(1,2),<1.
點(diǎn)評 本題考查了二次函數(shù)的性質(zhì):二次函數(shù)y=ax2+bx+c(a≠0)的頂點(diǎn)坐標(biāo)是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),對稱軸是直線x=-$\frac{b}{2a}$.當(dāng)a>0時(shí),拋物線y=ax2+bx+c(a≠0)的開口向上,x<-$\frac{b}{2a}$時(shí),y隨x的增大而減小;x>-$\frac{b}{2a}$時(shí),y隨x的增大而增大;x=-$\frac{b}{2a}$時(shí),y取得最小值$\frac{4ac-{b}^{2}}{4a}$,即頂點(diǎn)是拋物線的最低點(diǎn). 當(dāng)a<0時(shí),拋物線y=ax2+bx+c(a≠0)的開口向下,x<-$\frac{b}{2a}$時(shí),y隨x的增大而增大;x>-$\frac{b}{2a}$時(shí),y隨x的增大而減小;x=-$\frac{b}{2a}$時(shí),y取得最大值$\frac{4ac-{b}^{2}}{4a}$,即頂點(diǎn)是拋物線的最高點(diǎn).


 課課練江蘇系列答案
課課練江蘇系列答案 名牌中學(xué)課時(shí)作業(yè)系列答案
名牌中學(xué)課時(shí)作業(yè)系列答案 明天教育課時(shí)特訓(xùn)系列答案
明天教育課時(shí)特訓(xùn)系列答案 浙江新課程三維目標(biāo)測評課時(shí)特訓(xùn)系列答案
浙江新課程三維目標(biāo)測評課時(shí)特訓(xùn)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
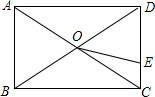 如圖,矩形ABCD,對角線AC,BD相交于點(diǎn)O,點(diǎn)E是邊CD上一動(dòng)點(diǎn),已知AC=10,CD=6,則OE的最小值是4.
如圖,矩形ABCD,對角線AC,BD相交于點(diǎn)O,點(diǎn)E是邊CD上一動(dòng)點(diǎn),已知AC=10,CD=6,則OE的最小值是4.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,在?ABCD中,E、F分別是AD、CD邊上的點(diǎn),連接BE、AF,它們相交于點(diǎn)G,延長BE交CD的延長線于點(diǎn)H,下列結(jié)論錯(cuò)誤的是( )
如圖,在?ABCD中,E、F分別是AD、CD邊上的點(diǎn),連接BE、AF,它們相交于點(diǎn)G,延長BE交CD的延長線于點(diǎn)H,下列結(jié)論錯(cuò)誤的是( )| A. | $\frac{AE}{ED}=\frac{BE}{EH}$ | B. | $\frac{EH}{EB}=\frac{DH}{CD}$ | C. | $\frac{EG}{BG}=\frac{AE}{BC}$ | D. | $\frac{AG}{FG}=\frac{BG}{GH}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
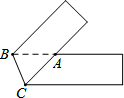 將一張寬為5cm的長方形紙片(足夠長)折疊成如圖所示圖形,重疊部分是一個(gè)三角形,則這個(gè)三角形面積的最小值是$\frac{25}{2}$cm2.
將一張寬為5cm的長方形紙片(足夠長)折疊成如圖所示圖形,重疊部分是一個(gè)三角形,則這個(gè)三角形面積的最小值是$\frac{25}{2}$cm2.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
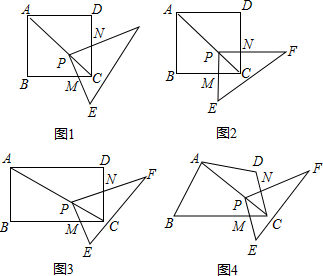
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
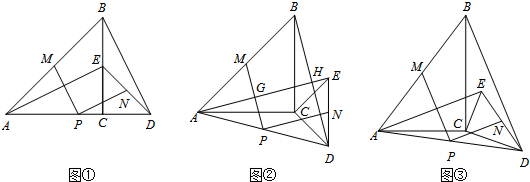
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
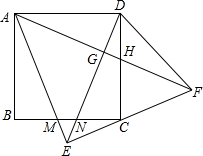 如圖,正方形ABCD中,以AD為底邊作等腰△ADE,將△ADE沿DE折疊,點(diǎn)A落到點(diǎn)F處,連接EF剛好經(jīng)過點(diǎn)C,再連接AF,分別交DE于G,交CD于H.在下列結(jié)論中:
如圖,正方形ABCD中,以AD為底邊作等腰△ADE,將△ADE沿DE折疊,點(diǎn)A落到點(diǎn)F處,連接EF剛好經(jīng)過點(diǎn)C,再連接AF,分別交DE于G,交CD于H.在下列結(jié)論中:| A. | 2個(gè) | B. | 3個(gè) | C. | 4個(gè) | D. | 5個(gè) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 為弘揚(yáng)中華傳統(tǒng)文化,某徽章設(shè)計(jì)公司設(shè)計(jì)了如圖所示的一種新式徽章,每件的成本是50元,為了合理定價(jià),先投放在某飾品店進(jìn)行試銷.試銷發(fā)現(xiàn),該徽章銷售單價(jià)為100元時(shí),每天的銷售量是50件,且當(dāng)銷售單價(jià)每降低1元時(shí),每天就可多售出5件.
為弘揚(yáng)中華傳統(tǒng)文化,某徽章設(shè)計(jì)公司設(shè)計(jì)了如圖所示的一種新式徽章,每件的成本是50元,為了合理定價(jià),先投放在某飾品店進(jìn)行試銷.試銷發(fā)現(xiàn),該徽章銷售單價(jià)為100元時(shí),每天的銷售量是50件,且當(dāng)銷售單價(jià)每降低1元時(shí),每天就可多售出5件.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com