
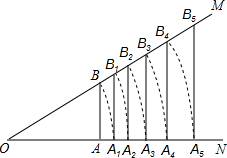
 如圖,已知∠MON=30°,AB⊥ON,垂足為點A,點B在射線OM上,AB=1cm,在射線ON上截取OA1=OB,過A1作A1B1∥AB,A1B1交射線OM于點B1,再在射線ON上截取OA2=OB1,過點A2作A2B2∥AB,A2B2交射線OM于點B2;…依次進行下去,則A1B1線段的長度為$\frac{2\sqrt{3}}{3}$,A6B6線段的長度為${2}^{6}(\frac{\sqrt{3}}{3})^{6}$.
如圖,已知∠MON=30°,AB⊥ON,垂足為點A,點B在射線OM上,AB=1cm,在射線ON上截取OA1=OB,過A1作A1B1∥AB,A1B1交射線OM于點B1,再在射線ON上截取OA2=OB1,過點A2作A2B2∥AB,A2B2交射線OM于點B2;…依次進行下去,則A1B1線段的長度為$\frac{2\sqrt{3}}{3}$,A6B6線段的長度為${2}^{6}(\frac{\sqrt{3}}{3})^{6}$. 分析 先根據30°角所對的直角邊等于斜邊的一半得出OB=2AB=2=OA1,再解直角三角形OA1B1,求出A1B1=$\frac{\sqrt{3}}{3}$OA1=$\frac{2\sqrt{3}}{3}$,同理,得出OB1=2A1B1=OA2,再解直角三角形OA2B2,求出A2B2=$\frac{\sqrt{3}}{3}$OA2=$\frac{{2}^{2}\sqrt{3}}{3}$•$\frac{\sqrt{3}}{3}$,由此得出A6B6線段的長度.
解答 解:在直角△OAB中,∵∠OAB=90°,∠AOB=30°,
∴OB=2AB=2,
∴OA1=OB=2,
在直角三角形OA1B1中,∵∠OA1B1=90°,∠A1OB1=30°,
∴A1B1=$\frac{\sqrt{3}}{3}$OA1=$\frac{2\sqrt{3}}{3}$,
∴OB1=2A1B1=OA2,
同理,在直角三角形OA2B2中,∵∠OA2B2=90°,∠A2OB2=30°,
∴A2B2=$\frac{\sqrt{3}}{3}$OA2=$\frac{{2}^{2}\sqrt{3}}{3}$$\frac{\sqrt{3}}{3}$,
…
∴A6B6=${2}^{6}(\frac{\sqrt{3}}{3})^{6}$.
故答案為$\frac{2\sqrt{3}}{3}$;${2}^{6}(\frac{\sqrt{3}}{3})^{6}$
點評 本題考查了直角三角形的知識及解直角三角形,難度中等,熟練掌握含30度角的直角三角形的性質:在直角三角形中,30°角所對的直角邊等于斜邊的一半是解題的關鍵.


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:初中數學 來源: 題型:填空題
 如圖,邊長為2的菱形ABCD中,∠BAD=60°,現有∠BFE=30°的三角板△BEF,將△BEF繞B旋轉得△BE′F′,BE′,BF′所在直線分別交線段AC于點M,N,若點C關于直線BE′的對稱點為C′,當C′N⊥AC時,AN的長為$\sqrt{3}$-1.
如圖,邊長為2的菱形ABCD中,∠BAD=60°,現有∠BFE=30°的三角板△BEF,將△BEF繞B旋轉得△BE′F′,BE′,BF′所在直線分別交線段AC于點M,N,若點C關于直線BE′的對稱點為C′,當C′N⊥AC時,AN的長為$\sqrt{3}$-1.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2.916×106米 | B. | 2.916×105米 | C. | 29.16×105米 | D. | 2.916×104米 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
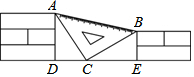 課間,小聰拿著老師的等腰直角三角板玩,不小心掉到兩墻之間(如圖),∠ACB=90°,AC=BC,從三角板的刻度可知AB=20cm,小聰很快就知道了砌墻磚塊的厚度的平方(每塊磚的厚度相等)為$\frac{200}{13}$cm.
課間,小聰拿著老師的等腰直角三角板玩,不小心掉到兩墻之間(如圖),∠ACB=90°,AC=BC,從三角板的刻度可知AB=20cm,小聰很快就知道了砌墻磚塊的厚度的平方(每塊磚的厚度相等)為$\frac{200}{13}$cm.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com