

分析 (1)如圖1中,作O′E⊥AB于E,MF⊥O′E于F.則四邊形AMFE是矩形,EF=AM=1.如圖2中,設切點為F,連接O′F,作O′E⊥OA于E,則四邊形O′EAF是矩形,在Rt△O′EM中,由sinα=$\frac{O′E}{O′M}$=$\frac{1}{2}$,推出α=60°.
(2)設切點為P,連接O′P,作MQ⊥O′P,則四邊形APQM是矩形.列出方程即可解決問題.
(3)設切點為P,連接O′P,作MQ⊥O′P,則四邊形APQM是矩形.列出方程即可解決問題、
(4)當半圓與射線AB相切時,之后開始出現兩個交點,此時α=90°;當N′落在AB上時,為半圓與AB有兩個交點的最后時刻,此時∵MN′=2AM,所以∠AMN′=60°,所以,α=120°因此,當半圓弧線與射線AB有兩個交點時,α的取值范圍是:90°<α≤120°.當N′落在AB上時,陰影部分面積最大,求出此時的面積即可.
解答 解:(1)如圖1中,作O′E⊥AB于E,MF⊥O′E于F.則四邊形AMFE是矩形,EF=AM=1.想辦法求出O′E的長即可.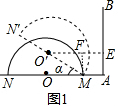
在Rt△MFO′中,∵∠MO$′\\;F$F=30°,MO′=2,
∴O′F=O′M•cos30°=$\sqrt{3}$,O′E=$\sqrt{3}$+1,
∴點O′到AB的距離為$\sqrt{3}$+1.
如圖2中,設切點為F,連接O′F,作O′E⊥OA于E,則四邊形O′EAF是矩形,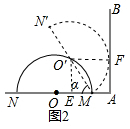
∴AE=O′F=2,
∵AM=1,
∴EM=1,
在Rt△O′EM中,sinα=$\frac{O′E}{O′M}$=$\frac{1}{2}$,
∴α=60°
故答案為$\sqrt{3}$+1,60°.
(2)設切點為P,連接O′P,作MQ⊥O′P,則四邊形APQM是矩形.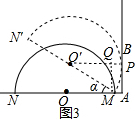
∵O′P=R,
∴R=$\frac{\sqrt{3}}{2}$R+1,
∴R=4+2$\sqrt{3}$.
(3)設切點為P,連接O′P,作MQ⊥O′P,則四邊形APQM是矩形.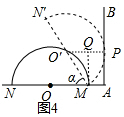
在Rt△O′QM中,O′Q=R•cosα,QP=m,
∵O′P=R,
∴R•cosα+m=R,
∴cosα=$\frac{R-m}{R}$.
故答案為$\frac{R-m}{R}$.
(4)如圖5中,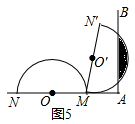
當半圓與射線AB相切時,之后開始出現兩個交點,此時α=90°;當N′落在AB上時,為半圓與AB有兩個交點的最后時刻,此時∵MN′=2AM,所以∠AMN′=60°,所以,α=120°因此,當半圓弧線與射線AB有兩個交點時,α的取值范圍是:90°<α≤120°
故答案為90°<α≤120°;
當N′落在AB上時,陰影部分面積最大,
所以S═$\frac{120•π•{m}^{2}}{360}$-$\frac{1}{2}$•$\sqrt{3}$m•$\frac{1}{2}$m=$\frac{π{m}^{2}}{3}$-$\frac{\sqrt{3}}{4}$m2.
點評 本題考查圓綜合題、旋轉變換、切線的判定和性質、解直角三角形等知識,解題的關鍵是學會添加常用輔助線,構造直角三角形或特殊四邊形解決問題,所以中考壓軸題.


 導學全程練創優訓練系列答案
導學全程練創優訓練系列答案科目:初中數學 來源: 題型:填空題
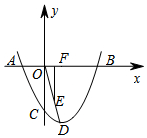 如圖,一拋物線經過點A(-2,0),B(6,0),C(0,-3),D為拋物線的頂點,過OD的中點E,作EF⊥x軸于點F,G為x軸上一動點,M為拋物線上一動點,N為直線EF上一動點,當以F、G、M、N為頂點的四邊形是正方形時,點G的坐標為(4-2$\sqrt{6}$,0)、(-4,0)、(4+2$\sqrt{6}$,0)或(4,0).
如圖,一拋物線經過點A(-2,0),B(6,0),C(0,-3),D為拋物線的頂點,過OD的中點E,作EF⊥x軸于點F,G為x軸上一動點,M為拋物線上一動點,N為直線EF上一動點,當以F、G、M、N為頂點的四邊形是正方形時,點G的坐標為(4-2$\sqrt{6}$,0)、(-4,0)、(4+2$\sqrt{6}$,0)或(4,0).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
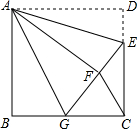 如圖,正方形ABCD中,AB=6,點E在邊CD上,且CD=3DE.將△ADE沿AE對折至△AFE,延長EF交邊BC于點G,連接AG,FC,下列結論:
如圖,正方形ABCD中,AB=6,點E在邊CD上,且CD=3DE.將△ADE沿AE對折至△AFE,延長EF交邊BC于點G,連接AG,FC,下列結論:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 有兩個不相等的實數根 | B. | 有兩個不相等的實數根 | ||
| C. | 無實數根 | D. | 無法確定 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com