
 如圖,在平面直角坐標系中,四邊形ABCD是矩形,AD∥x軸,A(-$\frac{9}{2}$,3 ),AB=2,AD=3.
如圖,在平面直角坐標系中,四邊形ABCD是矩形,AD∥x軸,A(-$\frac{9}{2}$,3 ),AB=2,AD=3.分析 (1)由四邊形ABCD是矩形,得到AB=CD=2,BC=AD=3,根據A(-$\frac{9}{2}$,3 ),AD∥x軸,即可得到B(-$\frac{9}{2}$,1),C(-$\frac{3}{2}$,1),D(-$\frac{3}{2}$,3);
(2)根據平移的性質將矩形ABCD向右平移m個單位,得到A′(-$\frac{9}{2}$+m,3),C(-$\frac{3}{2}$+m,1),由點A′,C′在反比例函數y=$\frac{k}{x}$ (x>0)的圖象上,得到方程 3×(-$\frac{9}{2}$+m)=1×(-$\frac{3}{2}$+m),即可求得結果.
解答 解:(1)∵四邊形ABCD是矩形,
∴AB=CD=2,BC=AD=3,
∵A(-$\frac{9}{2}$,3 ),AD∥x軸,
∴B(-$\frac{9}{2}$,1),C(-$\frac{3}{2}$,1),D(-$\frac{3}{2}$,3);
(2)∵將矩形ABCD向右平移m個單位,
∴A′(-$\frac{9}{2}$+m,3),C(-$\frac{3}{2}$+m,1),
∵點A′,C′在反比例函數y=$\frac{k}{x}$(x>0)的圖象上,
∴3×(-$\frac{9}{2}$+m)=1×(-$\frac{3}{2}$+m),
解得:m=6,
∴B′($\frac{9}{2}$,1),
∴k=$\frac{9}{2}$×1=$\frac{9}{2}$,
∴矩形ABCD的平移距離m=6,
反比例函數的解析式為:y=$\frac{9}{2x}$.
點評 本題考查了矩形的性質,圖形的變換-平移,反比例函數圖形上點的坐標特征,求反比例函數的解析式,掌握反比例函數圖形上點的坐標特征是解題的關鍵.


 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:初中數學 來源: 題型:解答題
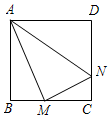 如圖,正方形ABCD邊長為8,M、N分別是BC、CD上的兩個動點,當M點在BC上運動時,始終保持AM和MN垂直,設BM=x,梯形ABCN的面積為y.
如圖,正方形ABCD邊長為8,M、N分別是BC、CD上的兩個動點,當M點在BC上運動時,始終保持AM和MN垂直,設BM=x,梯形ABCN的面積為y.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | BC=EF | B. | AB=DE | C. | ∠A=∠D | D. | ∠B=∠E |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
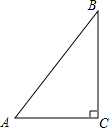 如圖,在Rt△ABC中,∠C=90°,AC=3,BC=4,則cosA的值為( )
如圖,在Rt△ABC中,∠C=90°,AC=3,BC=4,則cosA的值為( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
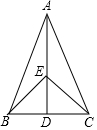 如圖,在△ABC中,AB=AC,點D是BC的中點,點E在AD上.
如圖,在△ABC中,AB=AC,點D是BC的中點,點E在AD上.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com