
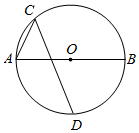
 如圖.AB是⊙O的直徑,∠BAC=60°,D為半圓的中點,若⊙O的半徑為4,求CD的長.
如圖.AB是⊙O的直徑,∠BAC=60°,D為半圓的中點,若⊙O的半徑為4,求CD的長. 分析 作輔助線,構建直角三角形,利用D為半圓的中點得等腰直角三角形AOD,求出AD的長,根據等腰三角形的性質得:∠ADE=30°,所以利用30°角所對的直角邊是斜邊的一半求AE的長,利用勾股定理求出DE的長,證明△ACE是等腰直角三角形,求出CE的長,相加即可得CD的長.
解答  解:連接AD、OD、OC,過A作AE⊥CD于E,
解:連接AD、OD、OC,過A作AE⊥CD于E,
∵D為半圓的中點,AB為⊙O的直徑,
∴∠AOD=90°,
∵AO=OD=4,
∴AD=4$\sqrt{2}$,∠ADO=45°,
∵OC=OA,∠BAC=60°,
∴△ACO是等邊三角形,
∴AC=AO=4,∠AOC=60°,
∴∠COD=60°+90°=150°,
∵OC=OD,
∴∠OCD=∠ODC=15°,
∴∠ADC=∠ADO-∠ODC=45°-15°=30°,
在Rt△AED中,AE=$\frac{1}{2}$AD=$\frac{1}{2}$×$4\sqrt{2}$=2$\sqrt{2}$,
由勾股定理得:DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{(4\sqrt{2})^{2}-(2\sqrt{2})^{2}}$=2$\sqrt{6}$,
∵∠ACO=60°,∠OCD=15°,
∴∠ACE=45°,
∴△ACE是等腰直角三角形,
∴CE=$\frac{AC}{\sqrt{2}}$=$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$,
∴CD=CE+ED=2$\sqrt{2}$+2$\sqrt{6}$.
點評 本題考查了圓周角定理、等腰三角形、等邊三角形的性質和判定,根據等腰三角形中等邊對等角和等邊三角形的性質求出特殊角的度數,利用勾股定理求邊的長度.


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:初中數學 來源: 題型:解答題
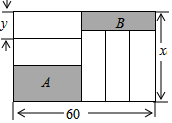 如圖,長為60cm,寬為x(cm)的大長方形被分割為7小塊,除陰影 A,B外,其余5塊是形狀、大小完全相同的小長方形,其較短一邊長為 y (cm).
如圖,長為60cm,寬為x(cm)的大長方形被分割為7小塊,除陰影 A,B外,其余5塊是形狀、大小完全相同的小長方形,其較短一邊長為 y (cm).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知線段AB,根據下列語句畫出圖形計算:
如圖,已知線段AB,根據下列語句畫出圖形計算:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
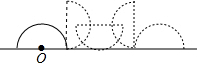 一個半圓形零件,直徑緊貼地面,現需要將零件按如圖所示方式,向前作無滑動翻轉,使圓心O再次落在地面上止.已知半圓的半徑為1m,則圓心O所經過的路線長是πm.(結果用π表示)
一個半圓形零件,直徑緊貼地面,現需要將零件按如圖所示方式,向前作無滑動翻轉,使圓心O再次落在地面上止.已知半圓的半徑為1m,則圓心O所經過的路線長是πm.(結果用π表示)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
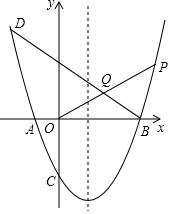 如圖,已知拋物線y=ax2+bx+c過點D(-2,5),與x軸交于點A(-1,0)和點B,與y軸交于點C(0,-3).
如圖,已知拋物線y=ax2+bx+c過點D(-2,5),與x軸交于點A(-1,0)和點B,與y軸交于點C(0,-3).查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 20 | B. | 24 | C. | 20或24 | D. | 24或26 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 已知a,b,c在數軸上的位置如圖所示,則下列結論正確的是( )
已知a,b,c在數軸上的位置如圖所示,則下列結論正確的是( )| A. | b表示負數,a,c表示正數,且|a|>|b| | B. | b表示負數,a,c表示正數,且|b|<|c| | ||
| C. | b表示負數,a,c表示正數,且|c|<|b| | D. | b表示負數,a,c表示正數,且|-a|>|b| |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com