
分析 根據銳角三角函數關系式,得sin2A+sin2B=1;根據一元二次方程根與系數的關系,得sinA+sinB=$\sqrt{2}$,sinA•sinB=-k,再進一步利用完全平方公式得到關于k的方程進行求解.
解答 解:∵sinA和sinB是方程x2-$\sqrt{2}$x-k=0的兩個根,
∴sinA+sinB=$\sqrt{2}$,sinA•sinB=-k,
∵Rt△ABC中,∠C=90°,
∴sin2A+sin2B=1,
∴2+2k=1,
解得,k=-$\frac{1}{2}$.
∵sinA+sinB=$\sqrt{2}$,sinA•sinB=$\frac{1}{2}$,
∴sinA=sinB=$\frac{\sqrt{2}}{2}$,
∴∠A=∠B=45°.
故答案為45°,45°,-$\frac{1}{2}$.
點評 此題綜合考查了一元二次方程根與系數的關系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的兩根時,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了銳角三角函數關系式.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
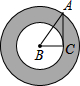 如圖,在Rt△ABC中,∠C=90°,將其繞B點順時針旋轉一周,則分別以BA,BC為半徑的圓形形成一圓環(陰影部分),為求該圓環的面積,只需測量一條線段的長度,這條線段就是( )
如圖,在Rt△ABC中,∠C=90°,將其繞B點順時針旋轉一周,則分別以BA,BC為半徑的圓形形成一圓環(陰影部分),為求該圓環的面積,只需測量一條線段的長度,這條線段就是( )| A. | AD | B. | AB | C. | BD | D. | AC |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 運算程序 | 例如 | 按左側的形式完成你的舉例 |
| ①給出任意一個三位數 | 325 | 123 |
| ②重復①中的數,得到一個新的數字 | 325325 | 123123 |
| ③將②的結果除以7 | 325325÷7=a46475 | 123123÷7=17589 |
| ④將③的結果除以11 | a÷11=b4225 | 17589÷11=1599 |
| ⑤將④的結果除以13 | b÷13=325 | 1599÷13=123 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
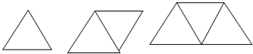 請你拿出火柴棒,現在我們來用火柴棒搭如圖所示的三角形.
請你拿出火柴棒,現在我們來用火柴棒搭如圖所示的三角形.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com