
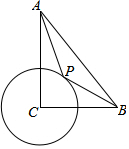
 如圖,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半徑為2,P為圓上一動點,連結AP,BP,AP+$\frac{1}{2}$BP的最小值為( )
如圖,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半徑為2,P為圓上一動點,連結AP,BP,AP+$\frac{1}{2}$BP的最小值為( )| A. | $\sqrt{37}$ | B. | 6 | C. | 2$\sqrt{17}$ | D. | 4 |
分析 首先連接CP,在CB上取點D,使CD=1,連結AD,則有$\frac{CD}{CP}$=$\frac{CP}{PB}$=$\frac{1}{2}$;然后根據相似三角形判定的方法,判斷出△PCD∽△BCP,即可推得$\frac{PD}{BP}$=$\frac{1}{2}$,AP+$\frac{1}{2}$BP=AP+PD,再應用勾股定理,求出AP+$\frac{1}{2}$BP的最小值為多少即可.
解答 解:如圖1,連接CP,在CB上取點D,使CD=1,連結AD,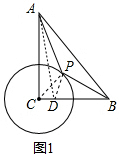 ,
,
∴$\frac{CD}{CP}$=$\frac{CP}{PB}$=$\frac{1}{2}$,
又∵∠PCD=∠BCP,
∴△PCD∽△BCP.
∴$\frac{PD}{BP}$=$\frac{1}{2}$,
∴PD=$\frac{1}{2}$BP,
∴AP+$\frac{1}{2}$BP=AP+PD,
當點A,P,D在同一條直線時,AP+$\frac{1}{2}$BP的值最小,
在Rt△ACD中,
∵CD=1,CA=6,
∴AD=$\sqrt{{1}^{2}{+6}^{2}}$=$\sqrt{37}$,
∴AP+$\frac{1}{2}$BP的最小值為$\sqrt{37}$.
故選:A.
點評 此題主要考查了最短路線問題,圓周角定理的應用,以及勾股定理的應用,要熟練掌握.


 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案 A加金題 系列答案
A加金題 系列答案科目:初中數學 來源: 題型:解答題
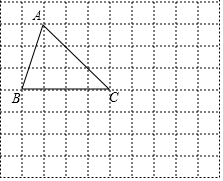 如圖,在由邊長為1個單位長度的小正方形組成的網格圖中有格點△ABC.(注:頂點在網格線交點處的三角形叫做格點三角形)
如圖,在由邊長為1個單位長度的小正方形組成的網格圖中有格點△ABC.(注:頂點在網格線交點處的三角形叫做格點三角形)查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,有一張長方形紙板,在它的四角各剪去一個同樣的正方形,然后將四周突出的部分折起,制成一個高為a的長方體形狀的無蓋紙盒.如果紙盒的容積為4a2b,底面長方形的一邊長為b(b<4a),求長方形紙板的面積.
如圖,有一張長方形紙板,在它的四角各剪去一個同樣的正方形,然后將四周突出的部分折起,制成一個高為a的長方體形狀的無蓋紙盒.如果紙盒的容積為4a2b,底面長方形的一邊長為b(b<4a),求長方形紙板的面積.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖是用八個全等的直角三角形拼接而成.記圖中正方形ABCD,正方形EFGH,正方形MNKT的面積分別為S1,S2,S3.若S1+S2+S3=16,則S2的值是$\frac{16}{3}$.
如圖是用八個全等的直角三角形拼接而成.記圖中正方形ABCD,正方形EFGH,正方形MNKT的面積分別為S1,S2,S3.若S1+S2+S3=16,則S2的值是$\frac{16}{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | a=5,b=-6 | B. | a=5,b=6 | C. | a=1,b=6 | D. | a=1,b=-6 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com