
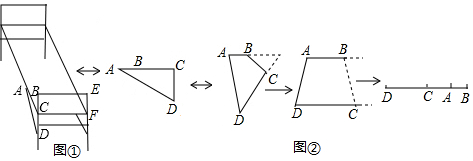
 如圖是用八個全等的直角三角形拼接而成.記圖中正方形ABCD,正方形EFGH,正方形MNKT的面積分別為S1,S2,S3.若S1+S2+S3=16,則S2的值是$\frac{16}{3}$.
如圖是用八個全等的直角三角形拼接而成.記圖中正方形ABCD,正方形EFGH,正方形MNKT的面積分別為S1,S2,S3.若S1+S2+S3=16,則S2的值是$\frac{16}{3}$. 分析 根據八個直角三角形全等,四邊形ABCD,EFGH,MNKT是正方形,得出CG=NG,CF=DG=NF,再根據S1=(CG+DG)2,S2=GF2,S3=(NG-NF)2,S1+S2+S3=16得出3GF2=16,求出GF2的值即可.
解答 解:∵八個直角三角形全等,四邊形ABCD,EFGH,MNKT是正方形,
∴CG=NG,CF=DG=NF,
∴S1=(CG+DG)2
=CG2+DG2+2CG•DG
=GF2+2CG•DG,
S2=GF2,
S3=(NG-NF)2=NG2+NF2-2NG•NF,
∴S1+S2+S3=GF2+2CG•DG+GF2+NG2+NF2-2NG•NF=3GF2=16,
∴GF2=$\frac{16}{3}$,
∴S2=$\frac{16}{3}$.
故答案為$\frac{16}{3}$.
點評 此題主要考查了勾股定理的應用,用到的知識點是勾股定理和正方形、全等三角形的性質,根據已知得出3GF2=16是解決問題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
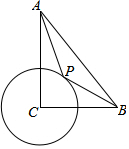 如圖,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半徑為2,P為圓上一動點,連結AP,BP,AP+$\frac{1}{2}$BP的最小值為( )
如圖,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半徑為2,P為圓上一動點,連結AP,BP,AP+$\frac{1}{2}$BP的最小值為( )| A. | $\sqrt{37}$ | B. | 6 | C. | 2$\sqrt{17}$ | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
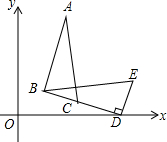 如圖,在△BDE中,∠BDE=90°,BD=3$\sqrt{2}$,點D的坐標是(5,0),∠BDO=15°,將△BDE旋轉得到△ABC的位置,點C在BD上,則過A、B、D三點圓的圓心坐標為($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$).
如圖,在△BDE中,∠BDE=90°,BD=3$\sqrt{2}$,點D的坐標是(5,0),∠BDO=15°,將△BDE旋轉得到△ABC的位置,點C在BD上,則過A、B、D三點圓的圓心坐標為($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
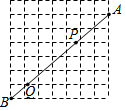 如圖,在7×7的正方形網格中,連接兩格點A,B,線段AB與其中兩條網格線的交點為P,Q,則AP:PQ:QB的值為( )
如圖,在7×7的正方形網格中,連接兩格點A,B,線段AB與其中兩條網格線的交點為P,Q,則AP:PQ:QB的值為( )| A. | 2:3:1 | B. | 4:5:3 | C. | 2:4:1 | D. | 5:6:3 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com