
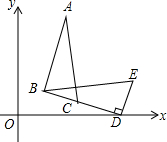
 如圖,在△BDE中,∠BDE=90°,BD=3$\sqrt{2}$,點D的坐標是(5,0),∠BDO=15°,將△BDE旋轉得到△ABC的位置,點C在BD上,則過A、B、D三點圓的圓心坐標為($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$).
如圖,在△BDE中,∠BDE=90°,BD=3$\sqrt{2}$,點D的坐標是(5,0),∠BDO=15°,將△BDE旋轉得到△ABC的位置,點C在BD上,則過A、B、D三點圓的圓心坐標為($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$). 分析 作線段AB與BD的垂直平分線,它們的交點即為過A、B、D三點圓的圓心P,連接PD、PB、PE,過P作PF⊥x軸于F,利用旋轉的性質得BC=DE,PB=PD,PE=PC,則可證明△PBC≌△PDE,所以∠PBC=∠PDE,易得∠PDB=∠PDE=$\frac{1}{2}$∠BDE=45°,于是可判斷△PBD為等腰直角三角形,則PD=BD=3,然后在Rt△PDF中利用含30度的直角三角形三邊的關系計算出DF和PF,從而可確定P點坐標.
解答 解:作線段AB與BD的垂直平分線,它們的交點即為過A、B、D三點圓的圓心P,連接PD、PB、PE,過P作PF⊥x軸于F,
∵△BDE旋轉得到△ABC的位置,點C在BD上,
∴BC=DE,PB=PD,PE=PC,
在△PBC和PDE中,
$\left\{\begin{array}{l}{PB=PD}\\{BC=DE}\\{PC=PE}\end{array}\right.$,
∴△PBC≌△PDE,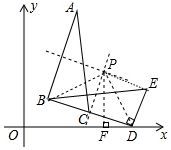
∴∠PBC=∠PDE,
而PB=PD,
∴∠PBD=∠PDB,
∴∠PDB=∠PDE=$\frac{1}{2}$∠BDE=45°,
∴△PBD為等腰直角三角形,
∴PD=$\frac{\sqrt{2}}{2}$BD=3,
∵∠BDO=15°,
∴∠PDO=45°+15°=60°,
∴∠DPF=30°,
∴DF=$\frac{1}{2}$PD=$\frac{1}{2}$×3=$\frac{3}{2}$,PF=$\sqrt{3}$DF=$\frac{3}{2}$$\sqrt{3}$,
∵點D的坐標是(5,0),
∴OF=OD-DF=5-$\frac{3}{2}$=$\frac{7}{2}$,
∴P點坐標為($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$),
故答案為:($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$).
點評 本題考查了三角形的外接圓與外心:經過三角形的三個頂點的圓,叫做三角形的外接圓.三角形外接圓的圓心是三角形三條邊垂直平分線的交點,叫做三角形的外心.解決本題的關鍵是證明△PBD為等腰直角三角形.


 53隨堂測系列答案
53隨堂測系列答案科目:初中數學 來源: 題型:解答題
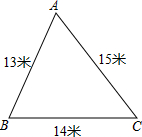 學校校內有一塊如圖所示的三角形空地ABC,計劃將這塊空地建成一個花園,以美化校園環境,預計花園每平方米造價為30元,學校修建這個花園需要投資多少元?
學校校內有一塊如圖所示的三角形空地ABC,計劃將這塊空地建成一個花園,以美化校園環境,預計花園每平方米造價為30元,學校修建這個花園需要投資多少元?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖是用八個全等的直角三角形拼接而成.記圖中正方形ABCD,正方形EFGH,正方形MNKT的面積分別為S1,S2,S3.若S1+S2+S3=16,則S2的值是$\frac{16}{3}$.
如圖是用八個全等的直角三角形拼接而成.記圖中正方形ABCD,正方形EFGH,正方形MNKT的面積分別為S1,S2,S3.若S1+S2+S3=16,則S2的值是$\frac{16}{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
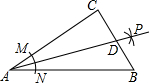 如圖,在Rt△ABC中,∠C=90°,以頂點A為圓心,適當長為半徑畫弧,分別交AC,AB于點M、N,再分別以點M、N為圓心,大于$\frac{1}{2}$MN的長為半徑畫弧,兩弧交于點P,作射線AB交邊BC于點D,若CD=4,AB=15,則△ABD的面積是30.
如圖,在Rt△ABC中,∠C=90°,以頂點A為圓心,適當長為半徑畫弧,分別交AC,AB于點M、N,再分別以點M、N為圓心,大于$\frac{1}{2}$MN的長為半徑畫弧,兩弧交于點P,作射線AB交邊BC于點D,若CD=4,AB=15,則△ABD的面積是30.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com