
分析 (1)根據新運算的定義式,代入數據求出結果即可;
(2)根據新運算的定義式將原式化簡為-x-8,代入x=-1即可得出結論.
解答 解:(1)$|\begin{array}{l}{6}&{0.5}\\{4}&{\frac{1}{2}}\end{array}|$=6×$\frac{1}{2}$-0.5×4=3-2=1;
$|\begin{array}{l}{-3}&{-2}\\{4}&{5}\end{array}|$=-3×5-(-2)×4=-15-(-8)=-7;
$|\begin{array}{l}{2}&{-3x}\\{3}&{-5x}\end{array}|$=2×(-5x)-(-3x)×3=-10x-(-9x)=-x.
故答案為:1;-7;-x.
(2)原式=(-3x2+2x+1)×(-2)-(-2x2+x-2)×(-3),
=(6x2-4x-2)-(6x2-3x+6),
=-x-8,
當x=-1時,原式=-x-8=-(-1)-8=-7.
∴當x=-1時,$|\begin{array}{l}{-3{x}^{2}+2x+1}&{-2{x}^{2}+x-2}\\{-3}&{-2}\end{array}|$的值為-7.
點評 本題考查了整式的化簡求值以及有理數的混合運算,讀懂題意掌握新運算并能用其將整式進行化簡是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
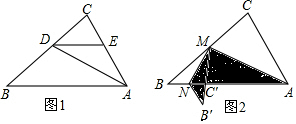
 如圖,以AB為直徑的⊙O中,CD是弦,CD∥AB,連接AC,BD交于點M.
如圖,以AB為直徑的⊙O中,CD是弦,CD∥AB,連接AC,BD交于點M.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
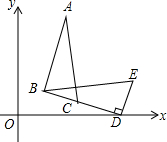 如圖,在△BDE中,∠BDE=90°,BD=3$\sqrt{2}$,點D的坐標是(5,0),∠BDO=15°,將△BDE旋轉得到△ABC的位置,點C在BD上,則過A、B、D三點圓的圓心坐標為($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$).
如圖,在△BDE中,∠BDE=90°,BD=3$\sqrt{2}$,點D的坐標是(5,0),∠BDO=15°,將△BDE旋轉得到△ABC的位置,點C在BD上,則過A、B、D三點圓的圓心坐標為($\frac{7}{2}$,$\frac{3}{2}$$\sqrt{3}$).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x(m-x)(n-x) | B. | x2(m-x)(n-x) | C. | $\frac{1}{3}$x(m-2n)(n-2x) | D. | x(m-2x)(n-2x) |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
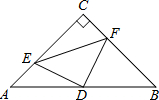 如圖,在△ABC中,∠C=90°,AC=BC=5,D是AB的中點,點E、F分別在AC、BC邊上運動(點E不與點A、C重合),且保持AE=CF,連接DE、DF、EF,在此運動變化的過程中,△CEF周長的最小值是5+$\frac{5\sqrt{2}}{2}$.
如圖,在△ABC中,∠C=90°,AC=BC=5,D是AB的中點,點E、F分別在AC、BC邊上運動(點E不與點A、C重合),且保持AE=CF,連接DE、DF、EF,在此運動變化的過程中,△CEF周長的最小值是5+$\frac{5\sqrt{2}}{2}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com