
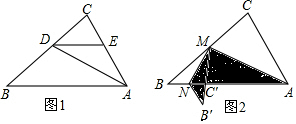
分析 (1)先判定三角形ADE是等腰三角形,再根據(jù)平行線分線段成比例定理,求得CE的長;
(2)先根據(jù)兩角對應相等,判定△ABC∽△NB′C′,再根據(jù)相似三角形的對應邊成比例,求得NC′與B′N的數(shù)量關系,最后結合BC′的長為2,求得NC′的長,進而得到AN的長度.
解答 解:(1)∵AD是∠BAC的平分線,DE∥AB,
∴∠EAD=∠BAD=∠EDA,
∴ED=EA,即△ADE是等腰三角形,
設CE=x,則AE=4-x=DE,
∵DE∥AB,
∴$\frac{DE}{BA}$=$\frac{CE}{CA}$,即$\frac{4-x}{6}$=$\frac{x}{4}$,
解得,CE=1.6,
∵DE∥AB,
∴$\frac{CD}{BD}$=$\frac{CE}{EA}$=$\frac{2}{3}$;
(2))由折疊得,∠B=∠B′,∠C=∠MC′A=∠B′C′N,AC=AC′=4,
∴△ABC∽△NB′C′,
∴$\frac{NC′}{NB′}$=$\frac{AC}{AB}$=$\frac{2}{3}$,
設NC′=2a,則BN=B′N=3a,
∵BC=AB-AC′=6-4=2,
∴NC′+BN=2,即2a+3a=2,
解得a=0.4,
∴NC′=2a=4.8,
∴AN=NC′+N′A=4.8.
點評 本題考查了平行線分線段成比例定理以及相似三角形的判定與性質,具有一定的難度.折疊是一種對稱變換,它屬于軸對稱,折疊前后圖形的形狀和大小不變,解題時應重點把握對應邊相等,對應角相等.


 優(yōu)質課堂快樂成長系列答案
優(yōu)質課堂快樂成長系列答案科目:初中數(shù)學 來源: 題型:選擇題
| A. | $\frac{1}{2^{98}}$尺 | B. | $\frac{1}{2^{99}}$尺 | C. | $\frac{1}{2^{100}}$尺 | D. | $\frac{1}{{2}^{101}}$尺 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
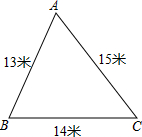 學校校內有一塊如圖所示的三角形空地ABC,計劃將這塊空地建成一個花園,以美化校園環(huán)境,預計花園每平方米造價為30元,學校修建這個花園需要投資多少元?
學校校內有一塊如圖所示的三角形空地ABC,計劃將這塊空地建成一個花園,以美化校園環(huán)境,預計花園每平方米造價為30元,學校修建這個花園需要投資多少元?查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com