

分析 (1)先求得∠BOC,再根據角平分線的性質得出∠COE,根據余角的性質得出∠DOE的度數;
(2)把數字換成希臘字母表示,同(1)的方法即可得出∠DOE的度數(用含α的代數式表示);
(3)結論是:∠DOE=$\frac{1}{2}$∠AOC.由平角的定義得出∠AOC+∠BOC=180°,再根據角平分線的性質得出∠COE=$\frac{1}{2}$∠BOC,即可代換出∠AOC與∠DOE的關系.
解答 解:(1)∵∠AOC+∠BOC=180°,
∴∠BOC=180°-∠AOC=180°-40°=140°,
∵OE平分∠BOC,
∴∠COE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×140°=70°,
∵∠COD是直角,∴∠COE+∠DOE=90°,
∴∠DOE=90°-∠COE=90°-70°=20°.
(2)若∠AOC=α,則∠DOE=$\frac{1}{2}$∠AOC=$\frac{α}{2}$.
(3)結論是:∠DOE=$\frac{1}{2}$∠AOC.
理由是:∵∠AOC+∠BOC=180°,
∴∠BOC=180°-∠AOC,
∵OE平分∠BOC,
∴∠COE=$\frac{1}{2}$∠BOC,
∵∠COD是直角,
∴∠COE+∠DOE=90°,
∴∠DOE=90°-∠COE=90°-$\frac{1}{2}$∠BOC
=90°-$\frac{1}{2}$(180°-∠AOC)
=$\frac{1}{2}$∠AOC.
點評 本題考查了角平分線的定義,是基礎題,難度不大,掌握各角之間的關系是解題的關鍵.


科目:初中數學 來源: 題型:解答題
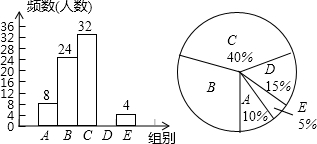 網絡技術的發展對學生學習方式產生巨大的影響,某校為了解學生每周課余利用網絡資源進行自主學習的時間,在本校隨機抽取若干名學生進行問卷調查,下面是根據調查結果繪制成的不完整的統計圖表:
網絡技術的發展對學生學習方式產生巨大的影響,某校為了解學生每周課余利用網絡資源進行自主學習的時間,在本校隨機抽取若干名學生進行問卷調查,下面是根據調查結果繪制成的不完整的統計圖表:| 組別 | 學習時間x(h) | 頻數(人數) |
| A | 0<x≤1 | 8 |
| B | 1<x≤2 | 24 |
| C | 2<x≤3 | 32 |
| D | 3<x≤4 | n |
| E | 4小時以上 | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 拋物線y=x2+4ax+b與x軸相交于O、A兩點(其中O為坐標原點),過點P(2,2a)作直線PM⊥x軸于點M,交拋物線于點B,點B關于拋物線對稱軸的對稱點為C(其中B、C不重合),連接AP交y軸于點N,連接BC和PC.
拋物線y=x2+4ax+b與x軸相交于O、A兩點(其中O為坐標原點),過點P(2,2a)作直線PM⊥x軸于點M,交拋物線于點B,點B關于拋物線對稱軸的對稱點為C(其中B、C不重合),連接AP交y軸于點N,連接BC和PC.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 40°50′=40.5° | |
| B. | 若線段AP=BP,則P一定是AB中點 | |
| C. | 若∠AOC=$\frac{1}{2}$∠AOB,則OC是∠AOB的平分線 | |
| D. | 連結兩點的線段的長度叫做兩點之間的距離 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com