
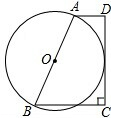
 如圖,在梯形ABCD中,AD∥BC,∠C=90°,AD+BC=AB,以AB為直徑作⊙O,求證:CD是⊙O的切線.
如圖,在梯形ABCD中,AD∥BC,∠C=90°,AD+BC=AB,以AB為直徑作⊙O,求證:CD是⊙O的切線. 分析 首先過點O作OE⊥CD于點E,易證得OE是梯形ABCD的中位線,可得OE=$\frac{1}{2}$(AD+BC),又由AD+BC=AB,以AB為直徑作⊙O.可得OE等于⊙O的半徑.
解答 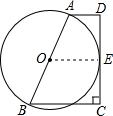 證明:過點O作OE⊥CD于點E,
證明:過點O作OE⊥CD于點E,
∵在梯形ABCD中,AD∥BC,∠C=90°,
∴AD⊥CD,BC⊥CD,
∴AD∥OE∥BC,
∵OA=OB,
∴OE是梯形ABCD的中位線,
∴OE=$\frac{1}{2}$(AD+BC),
∵AD+BC=AB,
∴OE=$\frac{1}{2}$AB,
∵以AB為直徑作⊙O.
∴直線CD是⊙O的切線.
點評 此題考查了切線的判定以及梯形的中位線的性質.此題難度適中,注意輔助線的作法,注意掌握數形結合思想的應用.


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
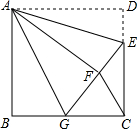 如圖,正方形ABCD中,AB=6,點E在邊CD上,且CD=3DE.將△ADE沿AE對折至△AFE,延長EF交邊BC于點G,連接AG,FC,下列結論:
如圖,正方形ABCD中,AB=6,點E在邊CD上,且CD=3DE.將△ADE沿AE對折至△AFE,延長EF交邊BC于點G,連接AG,FC,下列結論:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
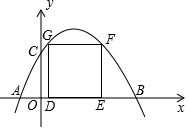 如圖,拋物線l與坐標軸的交點為A(-1,0),B(4,0),C(0,2),四邊形DEFG是正方形,且點D,E在x軸上,點F,G在拋物線上,則正方形DEFG的面積為57±8$\sqrt{41}$.
如圖,拋物線l與坐標軸的交點為A(-1,0),B(4,0),C(0,2),四邊形DEFG是正方形,且點D,E在x軸上,點F,G在拋物線上,則正方形DEFG的面積為57±8$\sqrt{41}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com