
 如圖,點P在△ABC的邊AC上,添加一個條件可判斷△ABP∽△ACB,其中添加不正確的是( )
如圖,點P在△ABC的邊AC上,添加一個條件可判斷△ABP∽△ACB,其中添加不正確的是( )| A. | ∠ABP=∠C | B. | ∠APB=∠ABC | C. | $\frac{AP}{AB}$=$\frac{AB}{AC}$ | D. | $\frac{AB}{AP}$=$\frac{CB}{BP}$ |
分析 根據相似三角形的判定方法,逐項判斷即可.
解答 解:
∵在△ABP和△ACB中,∠BAP=∠CAB,
∴當∠ABP=∠C時,滿足兩組角對應相等,可判斷△ABP∽△ACB,故A正確;
當∠APB=∠ABC時,滿足兩組角對應相等,可判斷△ABP∽△ACB,故B正確;
當$\frac{AP}{AB}$=$\frac{AB}{AC}$時,滿足兩邊對應成比例且夾角相等,可判斷△ABP∽△ACB,故C正確;
當$\frac{AB}{AP}$=$\frac{CB}{BP}$時,其夾角不相等,則不能判斷△ABP∽△ACB,故D不正確;
故選D.
點評 本題主要考查相似三角形的判定,掌握相似三角形的判定方法是解題的關鍵,即在兩個三角形中,滿足三邊對應成比例、兩邊對應成比例且夾角相等或兩組角對應相等,則這兩個三角形相似.


科目:初中數學 來源: 題型:填空題
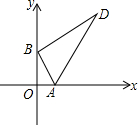 Rt△ABD的兩頂點A、B分別在x軸和y軸上運動,其中∠ABD=90°,∠D=30°,AB=4,則頂點D到原點O的距離的最小值為2$\sqrt{13}$-2,頂點D到原點O的距離的最大值為2$\sqrt{13}$+2.
Rt△ABD的兩頂點A、B分別在x軸和y軸上運動,其中∠ABD=90°,∠D=30°,AB=4,則頂點D到原點O的距離的最小值為2$\sqrt{13}$-2,頂點D到原點O的距離的最大值為2$\sqrt{13}$+2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
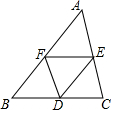 如圖,D、E、F是△ABC三邊的中點,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )
如圖,D、E、F是△ABC三邊的中點,且DE∥AB,DF∥AC,EF∥BC,平移△AEF可以得到的三角形是( )| A. | △BDF | B. | △DEF | C. | △CDE | D. | △BDF和△CDE |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
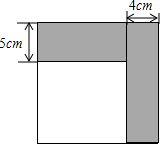 如圖所示,小明將一張正方形紙片剪去一條寬為4cm的長條后,再從剩下的長方形紙片上剪去一條寬為5cm的長條.如果兩次剪下的長條面積正好相等.
如圖所示,小明將一張正方形紙片剪去一條寬為4cm的長條后,再從剩下的長方形紙片上剪去一條寬為5cm的長條.如果兩次剪下的長條面積正好相等.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 各有一個角是45°的兩個等腰三角形 | |
| B. | 兩個等邊三角形 | |
| C. | 各有一個角是45°,腰長都是3cm的兩個等腰三角形 | |
| D. | 腰和頂角對應相等的兩個等腰三角形 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com