
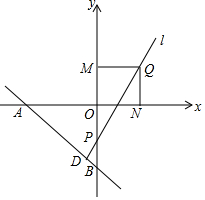
 如圖,在平面直角坐標系中,A(-8,0),B(0,-8),D為直線AB上一點,且D點橫坐標為-2,y軸上有一動點P,直線l經過D、P兩點.
如圖,在平面直角坐標系中,A(-8,0),B(0,-8),D為直線AB上一點,且D點橫坐標為-2,y軸上有一動點P,直線l經過D、P兩點.分析 (1)根據A(-8,0),B(0,-8),運用待定系數法求得直線AB的表達式,再根據D為直線AB上一點,且D點橫坐標為-2,求得D點坐標;
(2)當∠ADP=75°時,過點D作DC⊥y軸于點C,根據條件求得∠CPD=30°,得出DP=2CD=4,再根據勾股定理得到CP=2$\sqrt{3}$,最后根據OP=OB-PC-BC=8-2$\sqrt{3}$-2=6-2$\sqrt{3}$,即可得出P(0,2$\sqrt{3}$-6);
(3)存在點P(0,-4)或(0,$\sqrt{73}$-7).需要分兩種情況:①當直線l經過第一、三、四象限時,②當直線l經過第一、二、三象限時,分別根據待定系數法求得直線l表達式為y=$\frac{6}{m}$x+($\frac{12}{m}-6$),軸對稱直線l與坐標軸的交點坐標,最后根據所分成的三角形面積是△PDB面積的一半,列出方程進行計算即可得出m的值,進而得到P點坐標.
解答 解:(1)設直線AB解析式為y=kx+b,
把A(-8,0),B(0,-8)代入,得
$\left\{\begin{array}{l}{0=-8k+b}\\{-8=b}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=-8}\end{array}\right.$,
∴直線AB的表達式為y=-x-8,
∵D為直線AB上一點,且D點橫坐標為-2,
∴當x=-2時,y=2-8=-6,
∴D(-2,-6);
(2)當∠ADP=75°時,如圖1,過點D作DC⊥y軸于點C,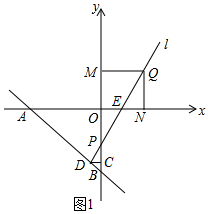
∵A(-8,0),B(0,-8),
∴△AOB是等腰直角三角形,
∴∠DBC=45°,OB=8,
∴∠BDC=45°,
∴∠CDP=180°-∠ADP-∠BDC=180°-75°-45°=60°,CD=CB=2,
∴Rt△CDP中,∠CPD=30°,
∴DP=2CD=4,
∴CP=2$\sqrt{3}$,
∴OP=OB-PC-BC=8-2$\sqrt{3}$-2=6-2$\sqrt{3}$,
∵點P在y軸負半軸上,
∴P(0,2$\sqrt{3}$-6);
(3)存在點P(0,-4)或(0,$\sqrt{73}$-7),使得直線DQ分長方形ONQM為兩部分,其中所分成的三角形面積是△PDB面積的一半.
分兩種情況:
①如圖1所示,當直線l經過第一、三、四象限時,設l與x軸交于點E,
∵Q點位于第一象限,且橫、縱坐標之積恰為12,
∴可設Q(m,$\frac{12}{m}$),
設直線l表達式為y=k'x+b',
把D(-2,-6)和Q(m,$\frac{12}{m}$)代入,得
$\left\{\begin{array}{l}{-6=-2k'+b'}\\{\frac{12}{m}=mk'+b'}\end{array}\right.$解得$\left\{\begin{array}{l}{k'=\frac{6}{m}}\\{b'=\frac{12}{m}-6}\end{array}\right.$,
∴直線l表達式為y=$\frac{6}{m}$x+($\frac{12}{m}-6$),
令x=0,則y=$\frac{12}{m}-6$,即P(0,$\frac{12}{m}-6$),此時BP=$\frac{12}{m}-6$-(-8)=$\frac{12}{m}$+2,
令y=0,則x=m-2,即E(m-2,0),此時NE=m-(m-2)=2,
∵△NQE面積是△PDB面積的一半,
∴$\frac{1}{2}$×NE×NQ=$\frac{1}{2}$×$\frac{1}{2}$BP×DC,
∴$\frac{1}{2}$×2×$\frac{12}{m}$=$\frac{1}{2}$×$\frac{1}{2}$×($\frac{12}{m}$+2)×2,
解得m=6,
∴P(0,-4);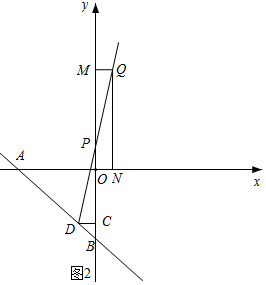
②如圖2所示,當直線l經過第一、二、三象限時,
同理可得P(0,$\frac{12}{m}-6$),
此時BP=$\frac{12}{m}-6$-(-8)=$\frac{12}{m}$+2,MP=$\frac{12}{m}$-($\frac{12}{m}-6$)=6,
∵△MQP面積是△PDB面積的一半,
∴$\frac{1}{2}$×MP×MQ=$\frac{1}{2}$×$\frac{1}{2}$BP×DC,
∴$\frac{1}{2}$×6×m=$\frac{1}{2}$×$\frac{1}{2}$×($\frac{12}{m}$+2)×2,
解得m=$\frac{1±\sqrt{73}}{6}$,
又∵m>0,
∴m=$\frac{1+\sqrt{73}}{6}$,
∴$\frac{12}{m}-6$=$\sqrt{73}$-7,
∴P(0,$\sqrt{73}$-7).
點評 本題屬于一次函數綜合題,主要考查了一次函數的圖象與性質,待定系數法求函數解析式,三角形的面積以及勾股定理的綜合應用,解決第(3)問的關鍵是畫出圖形,運用分類思想和方程思想進行求解.


 出彩同步大試卷系列答案
出彩同步大試卷系列答案科目:初中數學 來源: 題型:解答題
 如圖,已知等腰直角三角ACB的邊AC=BC=a,等腰直角三角形BED的邊BE=DE=b
如圖,已知等腰直角三角ACB的邊AC=BC=a,等腰直角三角形BED的邊BE=DE=b查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 類別/星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 平均數 |
| 甲 | 3 | 4 | 4 | 3 | 4 | 5 | 5 | |
| 乙 | 4 | 3 | 3 | 4 | 3 | 5 | 6 | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 在等邊△ABC中,點D在BC邊上,點E在AC的延長線上,DE=DA(如圖1)
在等邊△ABC中,點D在BC邊上,點E在AC的延長線上,DE=DA(如圖1)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com