
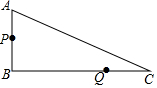
 如圖,在Rt△ABC中,∠B=90°,AB=7cm,AC=25cm.點P從點A沿AB方向以1cm/s的速度運動至點B,點Q從點B沿BC方向以6cm/s的速度運動至點C,P、Q兩點同時出發(fā).
如圖,在Rt△ABC中,∠B=90°,AB=7cm,AC=25cm.點P從點A沿AB方向以1cm/s的速度運動至點B,點Q從點B沿BC方向以6cm/s的速度運動至點C,P、Q兩點同時出發(fā).分析 (1)在直角△ABC中,根據(jù)勾股定理來求BC的長度;
(2)在直角△BPQ中,根據(jù)勾股定理來求PQ的長度;
(3)由路程=時間×速度求出AP,BQ,再根據(jù)等量關系:AP=CQ列出方程求解即可.
解答 解:(1)∵在Rt△ABC中,∠B=90°,AB=7cm,AC=25cm,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=24cm.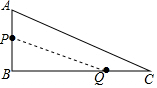 (2)如圖,連結PQ,
(2)如圖,連結PQ,
BP=7-2=5,
BQ=6×2=12,
在直角△BPQ中,由勾股定理得到:PQ=$\sqrt{B{P}^{2}+B{Q}^{2}}$=13(cm);
(3)設t秒后,AP=CQ.則
t=24-6t,
解得 t=$\frac{24}{7}$.
答:P、Q兩點運動$\frac{24}{7}$秒,AP=CQ.
點評 本題考查了勾股定理和一元一次方程的定義.解題時,需要熟悉路程=時間×速度,以及變形后的公式.


 亮點激活精編提優(yōu)100分大試卷系列答案
亮點激活精編提優(yōu)100分大試卷系列答案科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,⊙O的半徑為1,點A、P、B、C是⊙O上的四個點,∠APC=∠CPB=60°.
如圖,⊙O的半徑為1,點A、P、B、C是⊙O上的四個點,∠APC=∠CPB=60°.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 2πx2的系數(shù)是2 | B. | -xy2的次數(shù)為2 | C. | -5x2+x=-4x3 | D. | 3x2-x2=2x2 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
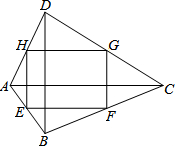 如圖,四邊形ABCD中,AC=8,BD=6,且AC⊥BD,連接四邊形ABCD各邊中點得到四邊形EFGH,下列說法正確的是( )
如圖,四邊形ABCD中,AC=8,BD=6,且AC⊥BD,連接四邊形ABCD各邊中點得到四邊形EFGH,下列說法正確的是( )| A. | 四邊形EFGH是矩形 | B. | 四邊形EFGH的周長是7 | ||
| C. | 四邊形EFGH的面積是24 | D. | 四邊形ABCD的面積是48 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
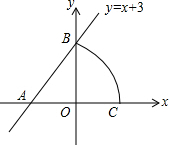 如圖,已知直線y=x+3與x軸交于點A,與y軸交于點B,以點A為圓心,AB為半徑畫弧,交x軸正半軸于點C,則點C坐標為( )
如圖,已知直線y=x+3與x軸交于點A,與y軸交于點B,以點A為圓心,AB為半徑畫弧,交x軸正半軸于點C,則點C坐標為( )| A. | (3$\sqrt{2}$-3,0) | B. | (3$\sqrt{2}$,0) | C. | (0,3$\sqrt{2}$-3) | D. | (3,0) |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com