
 如圖,⊙O的半徑為1,點A、P、B、C是⊙O上的四個點,∠APC=∠CPB=60°.
如圖,⊙O的半徑為1,點A、P、B、C是⊙O上的四個點,∠APC=∠CPB=60°.分析 (1)利用圓周角定理可得∠BAC=∠CPB,∠ABC=∠APC,而∠APC=∠CPB=60°,所以∠BAC=∠ABC=60°,證明△ABC是等邊三角形;
(2)在PC上截取PD=AP,則△APD是等邊三角形,然后證明△APB≌△ADC,證明BP=CD,即可證得;
(3)過點P作PE⊥AB,垂足為E,過點C作CF⊥AB,垂足為F,把四邊形的面積轉化為兩個三角形的面積進行計算,當點P為$\widehat{AB}$的中點時,PE+CF=PC從而得出最大面積.
解答 (1)在⊙O中,∠BAC與∠CPB是$\widehat{BC}$所對的圓周角,∠ABC與∠APC是$\widehat{AC}$所對的圓周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC為等邊三角形;
故答案為:等邊三角形;
(2)①如圖1,在PC上截取PD=AP,
又∵∠APC=60°,
∴△APD是等邊三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
$\left\{\begin{array}{l}{∠ABP=∠ACD}\\{∠APB=∠ADC}\\{AP=AD}\end{array}\right.$,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP,
故答案為:CP=BP+AP;
②當點P為$\widehat{AB}$的中點時,四邊形APBC的面積最大.
理由如下,如圖2,過點P作PE⊥AB,垂足為E.
過點C作CF⊥AB,垂足為F.
∵S△APB=$\frac{1}{2}$AB•PE,S△ABC=$\frac{1}{2}$AB•CF,
∴S四邊形APBC=$\frac{1}{2}$AB•(PE+CF),
當點P為$\widehat{AB}$的中點時,PE+CF=PC,PC為⊙O的直徑
∴此時四邊形APBC的面積最大.
又∵⊙O的半徑為1,
∴其內接正三角形的邊長AB=$\sqrt{3}$,
∴S四邊形APBC=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$.,
故答案為:$\sqrt{3}$.
點評 本題考查了圓周角定理、等邊三角形的判定、三角形的面積公式以及三角形的全等的判定與性質,正確作出輔助線,證明△APB≌△ADC是關鍵.


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
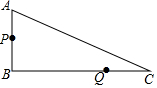 如圖,在Rt△ABC中,∠B=90°,AB=7cm,AC=25cm.點P從點A沿AB方向以1cm/s的速度運動至點B,點Q從點B沿BC方向以6cm/s的速度運動至點C,P、Q兩點同時出發(fā).
如圖,在Rt△ABC中,∠B=90°,AB=7cm,AC=25cm.點P從點A沿AB方向以1cm/s的速度運動至點B,點Q從點B沿BC方向以6cm/s的速度運動至點C,P、Q兩點同時出發(fā).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
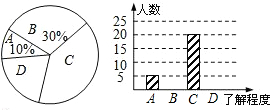
 所謂氣質,是指嬰兒出生后最早表示出來的以一種較為明顯而穩(wěn)定的人格特征類型,也指孩子對身體內在或外來刺激反應的方式.心理學界常將氣質分為四大類:膽汁型、多血質、黏液質、抑郁質.我校心理協(xié)會為了更好的了解學生,在高中隨機發(fā)放了若干份問卷調查,并將統(tǒng)計結果繪制成如圖表:
所謂氣質,是指嬰兒出生后最早表示出來的以一種較為明顯而穩(wěn)定的人格特征類型,也指孩子對身體內在或外來刺激反應的方式.心理學界常將氣質分為四大類:膽汁型、多血質、黏液質、抑郁質.我校心理協(xié)會為了更好的了解學生,在高中隨機發(fā)放了若干份問卷調查,并將統(tǒng)計結果繪制成如圖表:| 氣質類型 | 頻數 | 頻率 |
| 膽汁型 | 180 | a |
| 多血質 | 140 | 0.28 |
| 黏液質 | 80 | 0.16 |
| 抑郁質 | b | 0.20 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com