
分析 首先將原式分解因式,進而得出x,y的關系,進而化簡求出答案.
解答 解:∵x2-$\sqrt{2}$xy-4y2=0,
∴(x-2$\sqrt{2}$y)(x+$\sqrt{2}$y)=0,
∴x=2$\sqrt{2}$y,x=-$\sqrt{2}$y,
故當x=2$\sqrt{2}$y時,$\frac{{x}^{2}-\sqrt{2}xy+{y}^{2}}{{x}^{2}+\sqrt{2}xy+{y}^{2}}$=$\frac{4{y}^{2}+{y}^{2}}{(2\sqrt{2}y)^{2}+\sqrt{2}•2\sqrt{2}{y}^{2}+{y}^{2}}$=$\frac{5}{13}$,
當x=-$\sqrt{2}$y時,$\frac{{x}^{2}-\sqrt{2}xy+{y}^{2}}{{x}^{2}+\sqrt{2}xy+{y}^{2}}$=$\frac{5{y}^{2}}{(-\sqrt{2}y)^{2}+\sqrt{2}×(-\sqrt{2}y)•{y}^{2}+{y}^{2}}$=5.
點評 此題主要考查了二次根式的化簡求值,正確得出x,y的關系是解題關鍵.


 開心練習課課練與單元檢測系列答案
開心練習課課練與單元檢測系列答案科目:初中數學 來源:2016-2017學年湖北省枝江市八年級3月調研考試數學試卷(解析版) 題型:判斷題
已知x=2﹣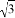 ,y=2+
,y=2+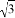 ,求下列代數式的值:
,求下列代數式的值:
(1)x2+2xy+y2;
(2)x2﹣y2.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
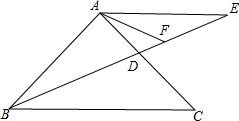 如圖,已知等腰△ABC中,AB=AC,點D是AC上一動點,點E在BD的延長線上,且AB=AE,AF平分∠CAE,交DE于F,∠ABC=45°,且BD平分∠ABC,請你證明,BD=2FE.
如圖,已知等腰△ABC中,AB=AC,點D是AC上一動點,點E在BD的延長線上,且AB=AE,AF平分∠CAE,交DE于F,∠ABC=45°,且BD平分∠ABC,請你證明,BD=2FE.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,⊙O的半徑為1,點A、P、B、C是⊙O上的四個點,∠APC=∠CPB=60°.
如圖,⊙O的半徑為1,點A、P、B、C是⊙O上的四個點,∠APC=∠CPB=60°.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com