
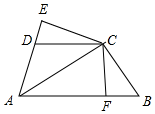
 如圖所示,AB∥DC,DC=CB,CE⊥AD,交AD的延長線于E,CF⊥AB垂足為F,∠DAB=∠B,求證:AC平分∠DAB.
如圖所示,AB∥DC,DC=CB,CE⊥AD,交AD的延長線于E,CF⊥AB垂足為F,∠DAB=∠B,求證:AC平分∠DAB. 分析 欲證明AC平分∠DAB,只要證明△CED≌△CFB,推出CE=CF,即可解決問題.
解答 證明:如圖,
∵∴CF⊥AB,CE⊥AE,
∴∠CED=∠CFB=90°,
∵CD∥AB,
∴∠EDC=∠DAB=∠B,
在△CED和△CFB中,
$\left\{\begin{array}{l}{∠CED=∠CFB}\\{∠CDE=∠B}\\{CD=CB}\end{array}\right.$,
∴△CED≌△CFB,
∴CE=CF,∵CF⊥AB,CE⊥AE,
∴AC是∠DAB的角平分線.
點評 本題考查全等三角形的判定和性質、角平分線的判定定理、平行線的性質等知識,解題的關鍵是熟練掌握角平分線的判定定理的應用,屬于中考常考題型.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源:2017屆山東省文慧學校九年級下學期第一次月考數學試卷(解析版) 題型:解答題
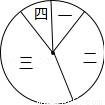
某校在踐行“社會主義核心價值觀”演講比賽中,對名列前20名的選手的綜合分數m進行分組統計,結果如表所示:
組號 | 分組 | 頻數 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
(1)求a的值;
(2)若用扇形圖來描述,求分數在8≤m<9內所對應的扇形圖的圓心角大小;
(3)將在第一組內的兩名選手記為:A1、A2,在第四組內的兩名選手記為:B1、B2,從第一組和第四組中隨機選取2名選手進行調研座談,求第一組至少有1名選手被選中的概率(用樹狀圖或列表法列出所有可能結果).
查看答案和解析>>
科目:初中數學 來源:2016-2017學年湖北省枝江市八年級3月調研考試數學試卷(解析版) 題型:單選題
△ABC中,AB=13cm,AC=15cm,高AD=12,則BC的長為( )
A. 14 B. 4 C. 14或4 D. 以上都不對
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
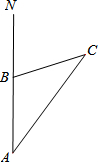 如圖,上午9時,一條船從A處出發,以20海里/時的速度向正北航行,12時到達B處,測得∠NAC=36°,∠ABC=108°,求從B處到燈塔C的距離.
如圖,上午9時,一條船從A處出發,以20海里/時的速度向正北航行,12時到達B處,測得∠NAC=36°,∠ABC=108°,求從B處到燈塔C的距離.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com