
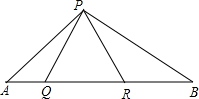
 如圖,△PQR為等邊三角形,∠APB=120°,若AQ=4,QR=6,則BR=9.
如圖,△PQR為等邊三角形,∠APB=120°,若AQ=4,QR=6,則BR=9. 分析 利用等邊三角形性質,進一步證得△AQP∽△PRB,再由三角形相似的性質解答即可.
解答 證明:∵△PQR是等邊三角形,
∴QR=PQ=PR,∠PQR=∠PRQ=∠QPR=60°,
∴∠AQP=∠PRB=120°,
∴∠A+∠APQ=60°,
又∵∠APB=120°,
∴∠A+∠B=60°,
∴∠APQ=∠B,
∴△AQP∽△PRB,
∴$\frac{PQ}{BR}=\frac{AQ}{PR}$,
∵QR=PQ=PR,
∴QR2=AQ•BR,
∴BR=$\frac{Q{R}^{2}}{AQ}$=$\frac{{6}^{2}}{4}$=9;
故答案為:9.
點評 此題主要考查等邊三角形的性質,三角形相似的判定與性質以及等量代換的滲透;證明三角形相似是解決問題的關鍵.


科目:初中數學 來源:2017屆湖北省襄陽市九年級下學期第一次月考數學試卷(解析版) 題型:單選題
下列命題正確的是( )
①三角形中最大內角一定不小于600;
② 所有等腰直角三角形都相似;
③正多邊形的外角為240,則它的中心角也為240;
④順次連接對角線相等的四邊形各邊中點得到矩形.
A. ①② B. ①②③ C. ②③④ D. ①②④
查看答案和解析>>
科目:初中數學 來源:2016-2017學年湖北省枝江市八年級3月調研考試數學試卷(解析版) 題型:解答題
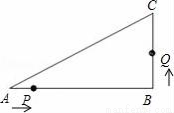
如圖,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,點P開始從點A開始沿△ABC的邊做逆時針運動,且速度為每秒1cm,點Q從點B開始沿△ABC的邊做逆時針運動,且速度為每秒2cm,他們同時出發,設運動時間我t秒.
(1)出發2秒后,求PQ的長;
(2)在運動過程中,△PQB能形成等腰三角形嗎?若能,則求出幾秒后第一次形成等腰三角形;若不能,則說明理由;
(3)從出發幾秒后,線段PQ第一次把直角三角形周長分成相等的兩部分?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
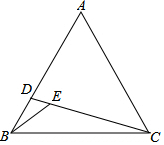 如圖,在等邊△ABC中,D為AB上一點,連接CD,在CD上取一點E,∠BEC=120°,連接BE.若CD=$\frac{14}{3}$,BE=2,△ACD的面積為$\frac{14}{3}$$\sqrt{3}$,則△BCE的面積為2$\sqrt{3}$.
如圖,在等邊△ABC中,D為AB上一點,連接CD,在CD上取一點E,∠BEC=120°,連接BE.若CD=$\frac{14}{3}$,BE=2,△ACD的面積為$\frac{14}{3}$$\sqrt{3}$,則△BCE的面積為2$\sqrt{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
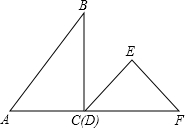 一副三角板如圖擺放,AC、DF在同一條直線上且點C、D重合,將三角板DEF沿CA方向以1cm/s的速度運動,當點D與點A重合時運動停止,已知AC=3cm,DF=4cm,設運動的時間為t(s),兩三角板重合部分的面積為S(cm2),下列圖象能大致反映S(cm2)與t(s)間函數關系的是( )
一副三角板如圖擺放,AC、DF在同一條直線上且點C、D重合,將三角板DEF沿CA方向以1cm/s的速度運動,當點D與點A重合時運動停止,已知AC=3cm,DF=4cm,設運動的時間為t(s),兩三角板重合部分的面積為S(cm2),下列圖象能大致反映S(cm2)與t(s)間函數關系的是( )| A. | 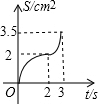 | B. | 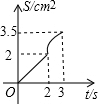 | C. | 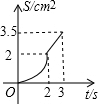 | D. | 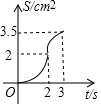 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com