
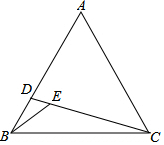
 如圖,在等邊△ABC中,D為AB上一點(diǎn),連接CD,在CD上取一點(diǎn)E,∠BEC=120°,連接BE.若CD=$\frac{14}{3}$,BE=2,△ACD的面積為$\frac{14}{3}$$\sqrt{3}$,則△BCE的面積為2$\sqrt{3}$.
如圖,在等邊△ABC中,D為AB上一點(diǎn),連接CD,在CD上取一點(diǎn)E,∠BEC=120°,連接BE.若CD=$\frac{14}{3}$,BE=2,△ACD的面積為$\frac{14}{3}$$\sqrt{3}$,則△BCE的面積為2$\sqrt{3}$. 分析 過(guò)B作BH⊥CD延長(zhǎng)線于點(diǎn)H,根據(jù)三角函數(shù)可求BH=$\sqrt{3}$,HE=1,再根據(jù)三角形面積公式得到AB=2$\sqrt{7}$,BD=$\frac{1}{3}$×2$\sqrt{7}$,根據(jù)勾股定理和線段的和差故關(guān)系可得CE=4,再根據(jù)三角形面積公式即可求解.
解答 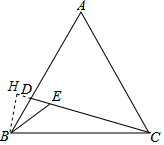 解:過(guò)B作BH⊥CD延長(zhǎng)線于點(diǎn)H,
解:過(guò)B作BH⊥CD延長(zhǎng)線于點(diǎn)H,
∵∠BEH=180°-120°=60°,BE=2,
∴BH=$\sqrt{3}$,HE=1,
S△BCD=$\frac{1}{2}$×$\sqrt{3}$×$\frac{14}{3}$=$\frac{7\sqrt{3}}{3}$,
∴S△BCA=$\frac{7\sqrt{3}}{3}$+$\frac{14\sqrt{3}}{3}$=7$\sqrt{3}$=$\frac{\sqrt{3}}{4}$AB2,
解得AB=2$\sqrt{7}$,
∴$\frac{{S}_{△BCD}}{{S}_{△BCA}}$=$\frac{2}{3}$=$\frac{AD}{AB}$,得BD=$\frac{1}{3}$×2$\sqrt{7}$,
在Rt△BDH中,DH=$\sqrt{B{D}^{2}-B{H}^{2}}$=$\frac{1}{3}$,DE=1-$\frac{1}{3}$=$\frac{2}{3}$,
CE=$\frac{14}{3}$-$\frac{2}{3}$=4,
∴S△BCE=$\frac{1}{2}$×$\sqrt{3}$×4=2$\sqrt{3}$.
故答案為:2$\sqrt{3}$.
點(diǎn)評(píng) 本題考查了勾股定理,等邊三角形的性質(zhì),三角形面積,求得BH,CE的長(zhǎng)是解題的關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源:2017屆湖北省襄陽(yáng)市九年級(jí)下學(xué)期第一次月考數(shù)學(xué)試卷(解析版) 題型:填空題
不等式組 的非負(fù)整數(shù)解是______.
的非負(fù)整數(shù)解是______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2016-2017學(xué)年湖北省武漢市侏儒山街四校八年級(jí)3月月考數(shù)學(xué)試卷(解析版) 題型:單選題
如圖,數(shù)軸上A,B兩點(diǎn)表示的數(shù)分別是1和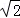 ,點(diǎn)A關(guān)于點(diǎn)B的對(duì)稱(chēng)點(diǎn)是點(diǎn)C,則點(diǎn)C所表示的數(shù)是( )
,點(diǎn)A關(guān)于點(diǎn)B的對(duì)稱(chēng)點(diǎn)是點(diǎn)C,則點(diǎn)C所表示的數(shù)是( )
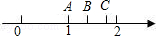
A. 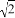 -1 B. 1+
-1 B. 1+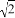 C. 2
C. 2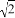 -2 D. 2
-2 D. 2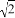 -1
-1
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源:2016-2017學(xué)年湖北省枝江市八年級(jí)3月調(diào)研考試數(shù)學(xué)試卷(解析版) 題型:單選題
等邊三角形的邊長(zhǎng)為2,則該三角形的面積為( )
A. 4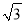 B.
B. 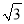 C. 2
C. 2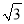 D. 3
D. 3
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
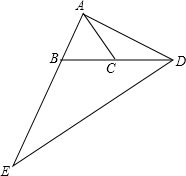 已知△ABC中,AB=AC,D為BC延長(zhǎng)線上一點(diǎn),且DC=BC,E是AB延長(zhǎng)線上的一點(diǎn),且BE=2AB,求證:DE=2AD.
已知△ABC中,AB=AC,D為BC延長(zhǎng)線上一點(diǎn),且DC=BC,E是AB延長(zhǎng)線上的一點(diǎn),且BE=2AB,求證:DE=2AD.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
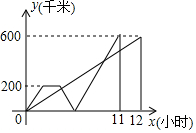 甲、乙兩車(chē)在依次連通A、B、C三地的公路上行駛,甲車(chē)從B地出發(fā)勻速向C地行駛,同時(shí)乙車(chē)人B地出發(fā)勻速向A地行駛,到達(dá)A地并在A地停留1小時(shí)后,調(diào)頭按原速向C地行駛.在兩車(chē)行駛的過(guò)程中,甲、乙兩車(chē)與B地的距離y(千米)與行駛時(shí)間x(小時(shí))之間的函數(shù)圖象如圖所示,當(dāng)甲、乙兩車(chē)相遇時(shí),所用時(shí)間為10小時(shí).
甲、乙兩車(chē)在依次連通A、B、C三地的公路上行駛,甲車(chē)從B地出發(fā)勻速向C地行駛,同時(shí)乙車(chē)人B地出發(fā)勻速向A地行駛,到達(dá)A地并在A地停留1小時(shí)后,調(diào)頭按原速向C地行駛.在兩車(chē)行駛的過(guò)程中,甲、乙兩車(chē)與B地的距離y(千米)與行駛時(shí)間x(小時(shí))之間的函數(shù)圖象如圖所示,當(dāng)甲、乙兩車(chē)相遇時(shí),所用時(shí)間為10小時(shí).查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題

| A. | 16 | B. | 10 | C. | 18 | D. | 20 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com