
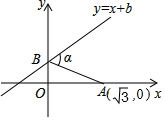
 如圖,已知A點坐標為($\sqrt{3}$,0),直線y=x+b(b>0)與y軸交于點B,連接AB,∠α=60°,則b的值為( )
如圖,已知A點坐標為($\sqrt{3}$,0),直線y=x+b(b>0)與y軸交于點B,連接AB,∠α=60°,則b的值為( )| A. | 3$\sqrt{3}$-3 | B. | $\sqrt{3}$+3 | C. | 2$\sqrt{3}$+3 | D. | 2$\sqrt{3}$-3 |
分析 令直線y=x+b與x軸交于點C,根據直線的解析式可求出點B、C的坐標,進而得出∠BCO=45°,再通過角的計算得出∠BAO=15°,以BA為邊在∠ABO內部作∠ABD=∠BAO=15°,可設AD=BD=x,得OD=OA-AD=$\sqrt{3}$-x,在Rt△BOD中根據cos∠BDO=$\frac{OD}{BD}$求得x,即可得BD的長,再根據BO=BDsin∠BDO可得答案.
解答 解:令直線y=x+b與x軸交于點C,
令y=x+b中x=0,則y=b,
∴B(0,b);
令y=x+b中y=0,則x=-b,
∴C(-b,0).
∴∠BCO=45°.
∵α=∠BCO+∠BAO=60°,
∴∠BAO=15°,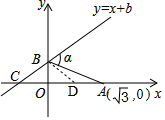
如圖,以BA為邊在∠ABO內部作∠ABD=∠BAO=15°,
設AD=BD=x,
∴OD=OA-AD=$\sqrt{3}$-x,
在Rt△BOD中,∵∠BDO=∠ABD+∠BAO=30°,
∴cos∠BDO=$\frac{OD}{BD}$,即$\frac{\sqrt{3}-x}{x}$=$\frac{\sqrt{3}}{2}$,
解得:x=4$\sqrt{3}$-6,即BD=4$\sqrt{3}$-6,
∴BO=BDsin∠BDO=(4$\sqrt{3}$-6)×$\frac{1}{2}$=2$\sqrt{3}$-3,
故選:D.
點評 本題主要考查三角形的外角性質、特殊角的三角函數值以及一次函數的斜率的幾何意義.解題時,注意挖掘隱含在題干中的已知條件∠BCA=45°及在直角三角形中構造30°的內角是解題的關鍵.


科目:初中數學 來源: 題型:解答題
 小東根據學習一次函數的經驗,對函數y=|2x-1|的圖象和性質進行了探究.下面是小東的探究過程,請補充完成:
小東根據學習一次函數的經驗,對函數y=|2x-1|的圖象和性質進行了探究.下面是小東的探究過程,請補充完成:| x | … | -2 | 0 | $\frac{1}{2}$ | 1 | m | … |
| y | … | 5 | 1 | 0 | 1 | n | … |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
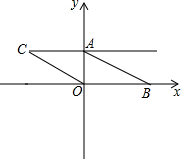 如圖.已知在平面直角坐標系中.點A(0,m),點B(n,0),D(2m,n),且m、n滿足(m-2)2+$\sqrt{n-4}$=0,將線段AB向左平移,使點B與點O重合,點C與點A對應.
如圖.已知在平面直角坐標系中.點A(0,m),點B(n,0),D(2m,n),且m、n滿足(m-2)2+$\sqrt{n-4}$=0,將線段AB向左平移,使點B與點O重合,點C與點A對應.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 RT△ABC中,∠ABC=30°,CD⊥AB,將△ACD繞A旋轉至△AC′D′,連接D′C,M、N分別是BC′和D′C的中點,連接MN,探索D′C和MN的數量及位置關系.
RT△ABC中,∠ABC=30°,CD⊥AB,將△ACD繞A旋轉至△AC′D′,連接D′C,M、N分別是BC′和D′C的中點,連接MN,探索D′C和MN的數量及位置關系.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
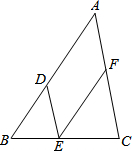 請在下列括號里填上合適的理由:
請在下列括號里填上合適的理由:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com