
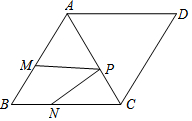
 已知菱形ABCD中,∠B=60°,AD=4$\sqrt{2}$,點P、M、N分別為AC、AB、BC上的動點,則PM+PN的最小值是2$\sqrt{6}$.
已知菱形ABCD中,∠B=60°,AD=4$\sqrt{2}$,點P、M、N分別為AC、AB、BC上的動點,則PM+PN的最小值是2$\sqrt{6}$. 分析 如圖,作AH⊥BC于H.首先證明△ABC,△ADC的是等邊三角形,作點M關于直線AC的對稱點M′,因為PM+PN=PM′+PN,所以欲求PM+PN是最小值,只要求PM′+PN的最小值,所以根據垂線段最短,當M″、P、N′共線時,M″N′⊥BC時,PM″+PN′的值最小,易證四邊形AHN′M″是矩形,所以N′M″=AH=AB•sin60°,由此即可解決問題.
解答 解:如圖,作AH⊥BC于H.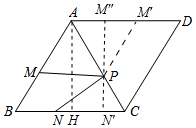
∵四邊形ABCD是菱形,
∴AB=BC=CD=AD,
∵∠B=∠D=60°,
∴△ABC,△ADC的是等邊三角形,
作點M關于直線AC的對稱點M′,
∵PM+PN=PM′+PN,
∴欲求PM+PN是最小值,只要求PM′+PN的最小值,
∴根據垂線段最短,
當M″、P、N′共線時,M″N′⊥BC時,PM″+PN′的值最小,
易證四邊形AHN′M″是矩形,
∴N′M″=AH=AB•sin60°=4$\sqrt{2}$•$\frac{\sqrt{3}}{2}$=2$\sqrt{6}$,
故答案為2$\sqrt{6}$.
點評 本題考查軸對稱最短問題、菱形的性質、等邊三角形的判定和性質、垂線段最短等知識,解題的關鍵是學會用轉化的思想思考問題,把最短問題轉化為垂線段最短,屬于中考常考題型.


 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案科目:初中數學 來源: 題型:選擇題
| A. | a=3,b=1 | B. | a=-3,b=1 | C. | a=3,b=-1 | D. | a=-3,b=-1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | a2•a5=a10 | B. | a2-2ab+b2=(a-b)2 | C. | -(a-b)=b-a | D. | 3a3b2÷a2b2=3a |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| 人員 | 經理 | 廚師 | 會計 | 保安 | 服務員 |
| 人數(人) | 1 | 2 | 1 | 1 | 5 |
| 工資(元) | 5000 | 4000 | 3500 | 3000 | 2000 |
| A. | 5000,3500 | B. | 5000,2500 | C. | 2000,3500 | D. | 2000,2500 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
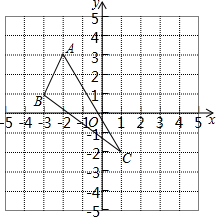 如圖,
如圖,查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{x-1}$ | B. | $\sqrt{18}$ | C. | $\sqrt{\frac{1}{16}}$ | D. | $\sqrt{9{a^2}}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
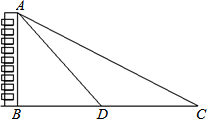 如圖,為了測量某建筑物AB高度,在平地上C處測得建筑物頂端A的仰角為30°,沿CB方向前進12m到達D處,在D處測得建筑物頂端A的仰角為45°,則建筑物AB高度等于(6$\sqrt{3}$+6)m.
如圖,為了測量某建筑物AB高度,在平地上C處測得建筑物頂端A的仰角為30°,沿CB方向前進12m到達D處,在D處測得建筑物頂端A的仰角為45°,則建筑物AB高度等于(6$\sqrt{3}$+6)m.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com