
 如圖,P是半徑為6的⊙O外一點,且PO=12,過P點作⊙O的兩條切線PA、PB,切點分別為點A、B,圖中陰影部分的面積是( )
如圖,P是半徑為6的⊙O外一點,且PO=12,過P點作⊙O的兩條切線PA、PB,切點分別為點A、B,圖中陰影部分的面積是( )| A. | 24π | B. | 18π | C. | 12π | D. | 6π |
分析 連接OP,由PA,PB是⊙O的切線,得到OA⊥PA,求得cos∠AOP=$\frac{OA}{AP}$=$\frac{1}{2}$,得到∠AOP=60°,同理∠OBP=60°,于是得到∠AOB=120°,根據扇形的面積公式即可得到結論.
解答 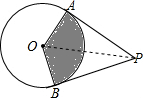 解:連接OP,
解:連接OP,
∵PA,PB是⊙O的切線,
∴OA⊥PA,
∵OA=6,OP=12,
∴cos∠AOP=$\frac{OA}{AP}$=$\frac{1}{2}$,
∴∠AOP=60°,
同理∠OBP=60°,
∴∠AOB=120°,
∴S扇形=$\frac{120•π×{6}^{2}}{360}$=12π.
故選C.
點評 此題考查了切線長的性質,直角三角形的性質,扇形面積公式等知識,熟記扇形的面積公式是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
 如圖,已知二次函數y=ax2+bx+c的圖象過A(2,0),B(0,-1)和C(4,5)三點.
如圖,已知二次函數y=ax2+bx+c的圖象過A(2,0),B(0,-1)和C(4,5)三點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖1,AD為正△ABC的高.
如圖1,AD為正△ABC的高.| 30° | 60° | |
| sin | $\frac{1}{2}$ | $\frac{\sqrt{3}}{2}$ |
| cos | $\frac{\sqrt{3}}{2}$ | $\frac{1}{2}$ |
| tan | $\frac{\sqrt{3}}{3}$ | $\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,拋物線y=-$\frac{1}{2}{x}^{2}$+bx+c經過點A(-2,0),C(4,0)兩點,和y軸相交于點B,連接AB、BC.
如圖,在平面直角坐標系中,拋物線y=-$\frac{1}{2}{x}^{2}$+bx+c經過點A(-2,0),C(4,0)兩點,和y軸相交于點B,連接AB、BC.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖所示,在1×2的正方形網格格點上已放置了兩枚棋子,如果第三枚棋子隨機放在其它格點上,那么以這三枚棋子所在的格點為頂點的三角形是直角三角形的概率為$\frac{3}{4}$.
如圖所示,在1×2的正方形網格格點上已放置了兩枚棋子,如果第三枚棋子隨機放在其它格點上,那么以這三枚棋子所在的格點為頂點的三角形是直角三角形的概率為$\frac{3}{4}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com