Question

4．如圖，已知二次函數y=ax²+bx+c的圖象過A（2，0），B（0，-1）和C（4，5）三點．
（1）求二次函數的解析式，對稱軸，頂點坐標；
（2）畫二次函數的圖象并標出圖象與x軸的另一個交點為D，求點D的坐標．

Answer 1

分析 （1）把A，B，C三點坐標代入二次函數解析式求出a，b，c的值，確定出二次函數解析式，進而求出對稱軸與頂點坐標即可；
（2）畫出二次函數圖象，標出點D，求出D坐標即可．

解答 解：（1）把A（2，0），B（0，-1），C（4，5）代入得：$\left\{\begin{array}{l}{4a+2b+c=0}\\{c=-1}\\{16a+4b+c=5}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{1}{2}}\\{c=-1}\end{array}\right.$，
則二次函數解析式為y=$\frac{1}{2}$x²-$\frac{1}{2}$x-1=$\frac{1}{2}$（x-$\frac{1}{2}$）²-$\frac{9}{8}$，即對稱軸為直線x=$\frac{1}{2}$，頂點坐標為（$\frac{1}{2}$，-$\frac{9}{8}$）；     
（2）如圖所示：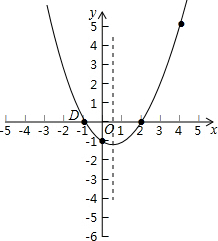

y=$\frac{1}{2}$x²-$\frac{1}{2}$x-1，令y=0，得到$\frac{1}{2}$x²-$\frac{1}{2}$x-1=0，
解得：x=2或x=-1，
則D（-1，0）．

點評 此題考查了拋物線與x軸的交點，二次函數的性質，以及待定系數法求二次函數解析式，熟練掌握二次函數的圖象與性質是解本題的關鍵．