Question

19．某農場計劃建一個養雞場，為了節約材料，決定利用原有的兩面互相垂直的墻（墻足夠長），另外的部分用30米的竹籬圍成，現有兩種方案：
①圍成一個矩形（如圖①）；
②圍成一個$\frac{1}{4}$圓（如圖②）．
設矩形的面積為S₁平方米，寬為x米，$\frac{1}{4}$圓的面積為S₂平方米，半徑為r米．
請你通過計算幫助農場主選擇一個圍成區域面積最大的方案（π取3）．

Answer 1

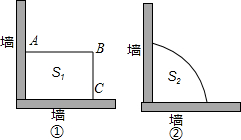
分析 根據題意表示出矩形的長，進而利用配方法求出二次函數最值，再求出扇形半徑，進而求出其面積．

解答 解：由題意可得：
方案一：設矩形的面積為S₁平方米，寬為x米，則另一邊長為：（30-x）m，根據題意可得：
S₁=x（30-x）=-x²+30x=-（x-15）²+225；
方案二：設$\frac{1}{4}$圓的面積為S₂平方米，半徑為r米，
則$\frac{90πr}{180}$=30，
則r=20，
根據題意可得：
S₂=$\frac{1}{4}$πr²=$\frac{1}{4}$×3×20²=300（平方米）．
答：方案二的面積較大．

點評 此題主要考查了二次函數的應用以及扇形面積求法，正確得出扇形半徑是解題關鍵．