
分析 根據相似三角形的判定,由已知可判定△ADB∽△BDC,進而求出∠A=∠CBD,即可求∠BCA的度數.
解答 解: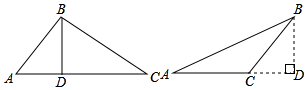 有兩種可能:△ABC為銳角三角形或鈍角三角形時,
有兩種可能:△ABC為銳角三角形或鈍角三角形時,
①當△ABC為銳角三角形時,
∵BD2=AD•CD,
∴$\frac{BD}{AD}=\frac{CD}{BD}$,
∵BD是AC邊上的高,
∴∠ADB=∠CDB=90°,
∴△ADB∽△BDC,
∴∠A=∠CBD,
∵∠A=38°,
∴∠CBD=38°,
∴∠BCA=∠BDC-∠CBD=90°-38°=52°.
②當△ABC為鈍角三角形時,
∵BD2=AD•CD,
∴$\frac{BD}{AD}=\frac{CD}{BD}$,
∵BD是AC邊上的高,
∴∠ADB=∠CDB=90°,
∴△ADB∽△BDC,
∴∠CBD=38°,
∴∠BCA=∠BDC+∠CBD=90°+38°=128°;
故答案為:52°或128°.
點評 本題考查相似三角形的判定與性質;熟練掌握相似三角形的判定與性質是解決問題的關鍵,注意分類討論.


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:初中數學 來源: 題型:選擇題
| A. | 6$\sqrt{2}$ | B. | 6$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
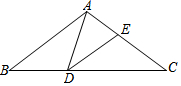 如圖,在△ABC中,AB=AC=10,在BC邊上取點D使BD=6,連結AD,以AD為一邊作∠ADE=∠B交邊AC于點E,如果sinB=$\frac{3}{5}$,則cos∠AED=$\frac{\sqrt{5}}{5}$.
如圖,在△ABC中,AB=AC=10,在BC邊上取點D使BD=6,連結AD,以AD為一邊作∠ADE=∠B交邊AC于點E,如果sinB=$\frac{3}{5}$,則cos∠AED=$\frac{\sqrt{5}}{5}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 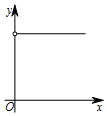 | B. | 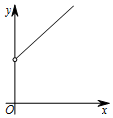 | C. | 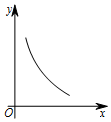 | D. |  |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com